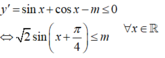Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng điều kiện có nghiệm của pt lượng giác bậc nhất, để pt đã cho vô nghiệm
\(\Leftrightarrow\left(2m+1\right)^2+\left(m+2\right)^2< \left(2m+3\right)^2\)
\(\Leftrightarrow5m^2+8m+5< 4m^2+12m+9\)
\(\Leftrightarrow m^2-4m-4< 0\)
\(\Leftrightarrow2-\sqrt{6}< m< 2+\sqrt{6}\)
\(\Rightarrow m=\left\{0;1;2;3;4\right\}\)
\(\Rightarrow\sum m=10\)

Lời giải:
Ta có:
\(\int ^{\frac{\pi}{2}}_{0}\frac{\sin x}{(\sin x+\cos x)^3}dx=\int ^{\frac{\pi}{2}}_{\frac{\pi}{4}}\frac{\sin x}{(\sin x+\cos x)^3}dx+\int ^{\frac{\pi}{4}}_{0}\frac{\sin x}{(\sin x+\cos x)^3}dx\)
\(=A+B\)
Xét riêng rẽ:
\(A=\int ^{\frac{\pi}{2}}_{\frac{\pi}{4}}\frac{\sin^3 x}{(\sin x+\cos x)^3}.\frac{dx}{\sin ^2x}=\int ^{\frac{\pi}{2}}_{\frac{\pi}{4}}\frac{1}{\left(\frac{\sin x+\cos x}{\sin x}\right)^3}d(-\cot x)\)
\(=\int ^{\frac{\pi}{2}}_{\frac{\pi}{4}}\frac{1}{(\cot x+1)^3}d(-\cot x)=-\int ^{\frac{\pi}{2}}_{\frac{\pi}{4}}\frac{d(\cot x+1)}{(\cot x+1)^3}\)
\(=\left.\begin{matrix} \frac{\pi}{2}\\ \frac{\pi}{4}\end{matrix}\right|\frac{1}{2(\cot x+1)^2}=\frac{3}{8}\)
\(B=\int ^{\frac{\pi}{4}}_{0}\frac{\sin x+\cos x-\cos x}{(\sin x+\cos x)^3}dx\)\(=\int ^{\frac{\pi}{4}}_{0}\frac{ 1}{(\sin x+\cos x)^2}dx-\int ^{\frac{\pi}{4}}_{0}\frac{\cos x}{(\sin x+\cos x)^3}dx\)
\(=\int ^{\frac{\pi}{4}}_{0}\frac{1}{\left(\frac{\sin x+\cos x}{\cos x}\right)^2}.\frac{dx}{\cos ^2x}-\int ^{\frac{\pi}{4}}_{0}\frac{1}{\left(\frac{\sin x+\cos x}{\cos^3 x}\right)^3}.\frac{dx}{\cos ^2x}\)
\(=\int ^{\frac{\pi}{4}}_{0}\frac{d(\tan x)}{(\tan x+1)^2}-\int ^{\frac{\pi}{4}}_{0}\frac{d(\tan x)}{(\tan x+1)^3}\)
\(=\int ^{\frac{\pi}{4}}_{0}\frac{d(\tan x+1)}{(\tan x+1)^2}-\int ^{\frac{\pi}{4}}_{0}\frac{d(\tan x+1)}{(\tan x+1)^3}\)
\(=\left.\begin{matrix} \frac{\pi}{4}\\ 0\end{matrix}\right|\frac{-1}{\tan x+1}+\left.\begin{matrix} \frac{\pi}{4}\\ 0\end{matrix}\right|\frac{1}{2(\tan x+1)^2}=\frac{1}{8}\)
Do đó: \(\int ^{\frac{\pi}{2}}_{0}\frac{\sin x}{(\sin x+\cos x)^3}dx=\frac{3}{8}+\frac{1}{8}=\frac{1}{2}\)
Sở dĩ phải chia tích phân thành tổng nhỏ như vậy là do khi ta thực hiện chia sin x xuống dưới mẫu thì hàm số không liên tục trong đoạn \([\frac{\pi}{2}; 0]\)