Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
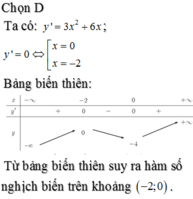
Đáp án C
Phương pháp:
Xác định khoảng mà tại đó y' ≤ 0, dấu “=” xảy ra ở hữu hạn điểm.
Cách giải:
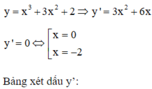
Hàm số nghịch biến trên khoảng (-2;0)
- Điều kiện đồng biến, nghịch biến của hàm số:
Cho hàm số y = f(x) có đạo hàm trên khoảng K.
+ f(x) đồng biến (tăng) trên K nếu f’(x) > 0 với ∀ x ∈ K.
+ f(x) nghịch biến (giảm) trên K nếu f’(x) < 0 với ∀ x ∈ K.
- Xét hàm số
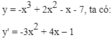
+ Hàm số đồng biến
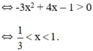
+ Hàm số nghịch biến
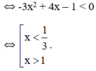
Vậy hàm số đồng biến trên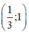 
nghịch biến trên các khoảng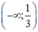 
và (1; +∞)
- Xét hàm số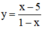 
Ta có: D = R \ {1}
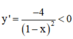∀ x ∈ D.
⇒ Hàm số nghịch biến trên từng khoảng (-∞; 1) và (1; +∞).
Ta có y ' = - 3 x 2 + 6 x + 3 m . Hàm số nghịch biến trên khoảng (0; +∞) nếu y' ≤ 0 trên khoảng (o; +∞)
Cách 1: Dùng định lí dấu tam thức bậc hai.
Xét phương trình - 3 x 2 + 6 x + 3 m . Ta có Δ' = 9(1 + m)
TH1: Δ' ≤ 0 => m ≤ -1 khi đó, - 3 x 2 + 6 x + 3 m < 0 nên hàm số nghịch biến trên R .
TH2: Δ' > 0 => m > -1; y' = 0 có hai nghiệm phân biệt là x = 1 ±√(1+m) .
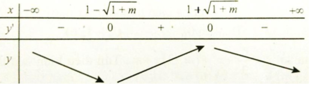
Hàm số nghịch biến trên (0; +∞) <=> 1 + √(1+m) ≤ 0, vô lí.
Từ TH1 và TH2, ta có m ≤ -1
Cách 2: Dùng phương pháp biến thiên hàm số.
Ta có y ' = - 3 x 2 + 6 x + 3 m ≤ 0 , ∀x > 0 <=> 3 m ≤ 3 x 2 - 6 x , ∀x > 0
Từ đó suy ra 3 m ≤ m i n ( 3 x 2 - 6 x ) với x > 0
Mà 3 x 2 - 6 x = 3 ( x 2 - 2 x + 1 ) - 3 = 3 ( x - 1 ) 2 - 3 ≥ - 3 ∀ x
Suy ra: m i n ( 3 x 2 – 6 x ) = - 3 khi x= 1
Do đó 3m ≤ -3 hay m ≤ -1.
Chọn đáp án C.
Đáp án D
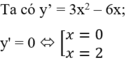
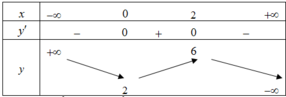
Xét dấu y’ suy ra hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞)
TXĐ: R \ {2}
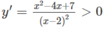
(do x 2 − 4x + 7 x 2 − 4x + 7 có ∆ ' = - 3 < 0)
Vậy hàm số đã cho đồng biến trên các khoảng (− ∞ ;2),(2;+ ∞ )
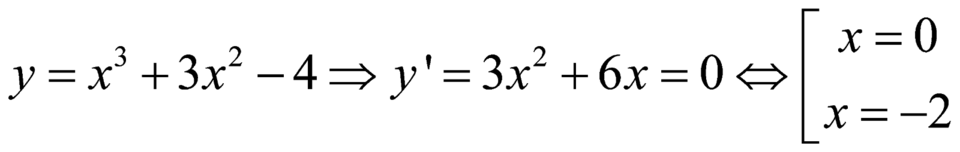
a.
\(y'=4x^3+8x=4x\left(x^2+2\right)=0\Rightarrow x=0\)
Dấu của y':
Hàm đồng biến trên \(\left(0;+\infty\right)\) và nghịch biến trên \(\left(-\infty;0\right)\)
b.
\(y'=3x^2+6x+3=3\left(x+1\right)^2\ge0\) ; \(\forall x\)
\(\Rightarrow\) Hàm đồng biến trên R