
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi số thứ nhất là x. Như vậy thì số thứ hai là 20-x.
Ta có phương trình \(x^2+\left(20-x\right)^2=280\Leftrightarrow2x^2-40x+120=0\Leftrightarrow x^2-20x+60=0\Rightarrow x=10\pm2\sqrt{10}\)
Vậy hai số đó là \(10+2\sqrt{10}\)và\(10-2\sqrt{10}\)

Có : 185 = x^2 + (x-3)^2 = x^2+x^2-6x+9 = 2x^2-6x+9
<=> 2x^2-6x+9-185 = 0
<=> 2x^2-6x-176 = 0
<=> x^2-3x-88 = 0
<=> (x^2-11x)+(8x-88) = 0
<=> (x-11).(x+8) = 0
<=> x-11=0 hoặc x+8=0
<=> x=11 hoặc x=-8
<=> x=11 ( vì x > 0 )
Vậy x = 11
Tk mk nha


Gọi hai số cần tìm là x, y.
Theo đề bài ta có:
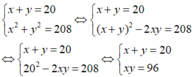
Suy ra x, y là nghiệm của phương trình:
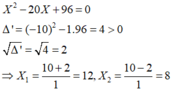
Vậy hai số cần tìm là 12 và 8

Ta có \(x^2+9x+20=0\Leftrightarrow\left(x+4\right)\left(x+5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=-5\end{matrix}\right.\).
Xét 2 TH:
+) a + b = -4; ab = -5: Theo định lý Viet đảo ta có a, b là hai nghiệm của pt \(t^2+4t-5=0\Leftrightarrow\left(t-1\right)\left(t+5\right)=0\Leftrightarrow\left[{}\begin{matrix}t=1\\t=-5\end{matrix}\right.\)
+) a + b = -5; ab = -4: Bạn giải tương tự.
