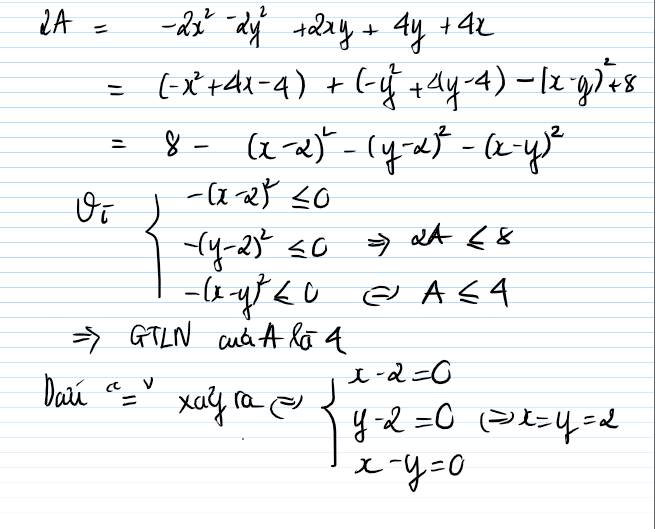Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\text{Đặt: }A=-x^2-y^2+xy+2x+2y.\)
\(\Rightarrow2A=-2x^2-2y^2+2xy+4x+4y=-\left(x^2-4x+4\right)-\left(y^2-y+4\right)-\left(x^2-2xy+y^2\right)+8\)
\(=8-\left(x-2\right)^2-\left(y-2\right)^2-\left(x-y\right)^2\)

(x2/2 - xy + y2 /2) + (x2 /2 - 2x + 2) + (y2 /2 - 2y + 2) - 4 = (x/√2 - y √2)2 + (x/√2 - √2)2 + (y/√2 - √2)2 - 4 >= -4
Vậy GTNN là -4 đạt được khi x = y = 2

\(B=-x^2-y^2+xy+2x+2y\)
\(\Rightarrow-2B=2x^2+2y^2-2xy-2x-4y\)
\(=\left(x^2-2xy+y^2\right)+\left(x^2-4x+4\right)+\left(y^2-4y+4\right)-8\)
\(=\left(x-y\right)^2+\left(x-2\right)^2+\left(y-2\right)^2-8\)
vì \(\left(x-y\right)^2\ge0\forall x,y;\left(x-2\right)^2\ge0\forall x;\left(y-2\right)\ge0\forall y\)nên
\(-2B=\left(x-y\right)^2+\left(x-2\right)^2+\left(y-2\right)^2-8\ge8\)
hay \(-2B\ge-8\Rightarrow B\le4\)
\(\Rightarrow maxB=4\Leftrightarrow\hept{\begin{cases}x-y=0\\x-2=0\\y-2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=y\\x=2\\y=2\end{cases}}}\)


Đặt A = -x2 - y2 + xy + 2x + 2y
=> 4A = -4x2 - 4y2 + 4xy + 8x + 8y
= -(4x2 - 4xy + y2) + 4(2x - y) - 4 - 3y2 + 12y - 12 + 16
= -(2x - y)2 + 4(2x - y) - 4 - 3(y2 - 4y + 4) + 16
= -(2x - y - 2)2 - 3(y - 2)2 + 4 \(\le16\)
=> A \(\le4\)
=> Max A = 4
Dấu "=" xảy ra <=> \(\hept{\begin{cases}2x-y-2=0\\y-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=2\end{cases}}\)
Vậy Max A = 4 <=> x = y = 2