K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 1 2022
a: Thay x=1 và y=-2 vào y=ax+1, ta được:
a+1=-2
hay a=-3
Vậy: (d'): y=-3x+1
c: Tọa độ giao điểm của (d) và (d') là:
\(\left\{{}\begin{matrix}-3x+1=x+3\\y=x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=3-\dfrac{1}{2}=\dfrac{5}{2}\end{matrix}\right.\)
PN
1
22 tháng 10 2023
Xét ΔADB có \(\widehat{ADC}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADC}=\widehat{BAD}+\widehat{B}\)
Xét ΔADC có \(\widehat{ADB}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADB}=\widehat{CAD}+\widehat{C}=\widehat{BAD}+\widehat{C}\)
\(\widehat{ADC}-\widehat{ADB}\)
\(=\widehat{BAD}+\widehat{B}-\widehat{BAD}-\widehat{C}\)
\(=\widehat{B}-\widehat{C}=20^0\)
mà \(\widehat{ADC}+\widehat{ADB}=180^0\)
nên \(\widehat{ADC}=\dfrac{180^0+20^0}{2}=100^0\)
4 tháng 12 2021
\(a,\Leftrightarrow3m-1=-2\Leftrightarrow m=-\dfrac{1}{3}\Leftrightarrow\left(d\right):y=-\dfrac{1}{3}x-1\\ c,\text{Hs góc: }-\dfrac{1}{3}\\ \text{Gọi góc cần tìm là }\alpha>90^0\\ \Leftrightarrow\tan\left(180^0-\alpha\right)=\dfrac{1}{3}\approx\tan18^0\\ \Leftrightarrow\alpha\approx180^0-18^0=162^0\)
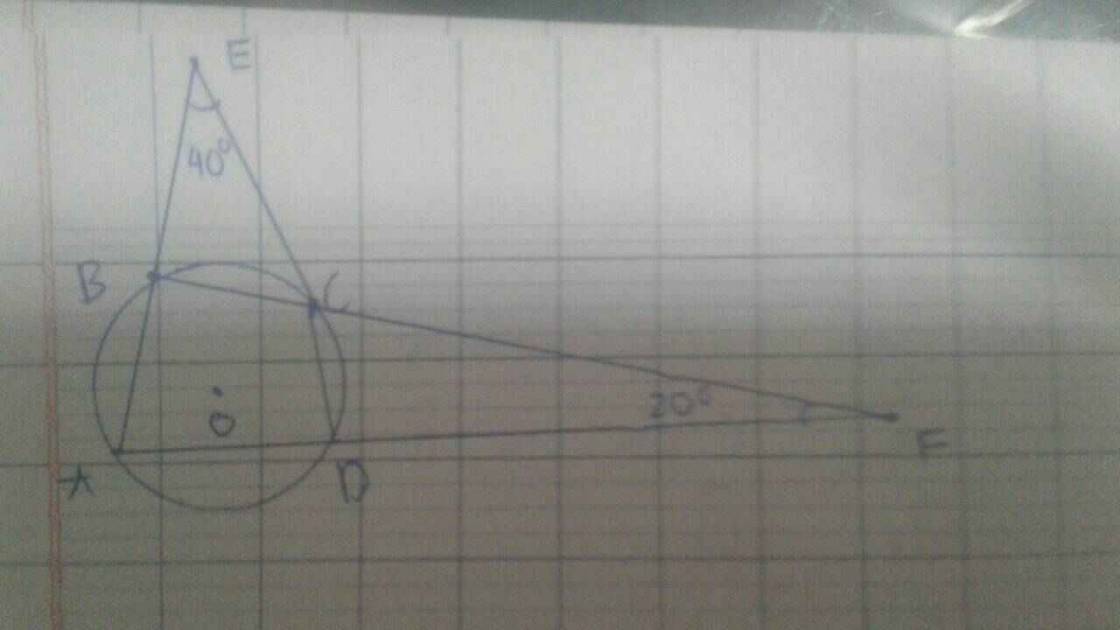
Áp dụng định lý về tổng 3 góc trong tam giác và định lý tứ giác nội tiếp, ta có:
\(\left\{{}\begin{matrix}A+B=180^0-20^0\\A+D=180^0-40^0\\B+D=180^0\\\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A+B=160^0\\A+D=140^0\\B+D=180^0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2A+B+D=300^0\\B+D=180^0\end{matrix}\right.\)
\(\Rightarrow2A+180^0=300^0\)
\(\Rightarrow A=60^0\)
\(\Rightarrow B=160^0-A=100^0\)
\(C=180^0-A=120^0\)
\(D=180^0-B=80^0\)