Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=12^2-6^2=108\)
hay \(AC=6\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{1}{2}\)
\(\Leftrightarrow\widehat{C}=30^0\)
hay \(\widehat{B}=60^0\)

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\)
=>\(\widehat{B}\simeq53^0\)
=>\(\widehat{C}\simeq37^0\)
b: Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
=>\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{10}{7}\)
=>\(DB=\dfrac{30}{7}\left(cm\right);DC=\dfrac{40}{7}\left(cm\right)\)

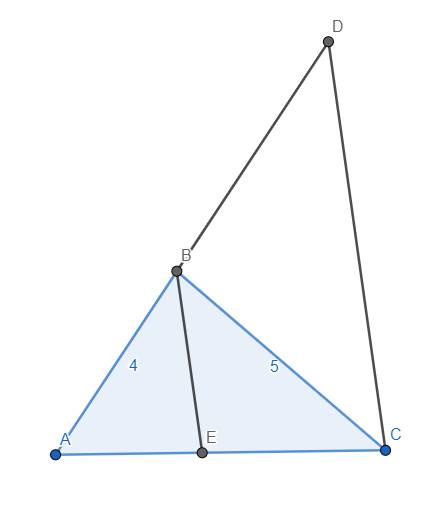
a) Xét tam giác ACB và ADC, có \(\widehat{A}\) chung và \(\widehat{ACB}=\widehat{ADC}\left(gt\right)\), suy ra đpcm.
b) Từ câu a) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AC}{AD}\) \(\Rightarrow AC^2=AB.AD\)
Kẻ phân giác BE của tam giác ABC. Vì \(\widehat{B}=2\widehat{C}\) nên \(\widehat{ABE}=\widehat{ADC}\) hay BE//CD. Mặt khác, \(\dfrac{EA}{EC}=\dfrac{BA}{BC}=\dfrac{4}{5}\) nên suy ra \(\dfrac{BA}{BD}=\dfrac{4}{5}\Leftrightarrow\dfrac{4}{BD}=\dfrac{4}{5}\Leftrightarrow BD=5\), suy ra \(AD=AB+BD=4+5=9\).
\(\Rightarrow AC^2=AB.AD=4.9=36\) \(\Rightarrow AC=6\).
Vậy \(AC=6\)
Dạ thưa cô, cái này em áp dụng tính chất đường phân giác trong tam giác ạ. Cái này lớp 9 được dùng luôn không cần chứng minh ạ.

Câu hỏi của •Ƙ - ƔℌŤ⁀ᶦᵈᵒᶫ - Toán lớp 7 - Học toán với OnlineMath
Thay I bằng M
Tham khảo link này : https://olm.vn/hoi-dap/detail/229494383404.html
Xét ΔADB có \(\widehat{ADC}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADC}=\widehat{BAD}+\widehat{B}\)
Xét ΔADC có \(\widehat{ADB}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADB}=\widehat{CAD}+\widehat{C}=\widehat{BAD}+\widehat{C}\)
\(\widehat{ADC}-\widehat{ADB}\)
\(=\widehat{BAD}+\widehat{B}-\widehat{BAD}-\widehat{C}\)
\(=\widehat{B}-\widehat{C}=20^0\)
mà \(\widehat{ADC}+\widehat{ADB}=180^0\)
nên \(\widehat{ADC}=\dfrac{180^0+20^0}{2}=100^0\)