K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 2 2017
bài này ta có thể giải theo 2 cách
ta có A = \(\frac{x^2-2x+2011}{x^2}\)
= \(\frac{x^2}{x^2}\)- \(\frac{2x}{x^2}\)+ \(\frac{2011}{x^2}\)
= 1 - \(\frac{2}{x}\)+ \(\frac{2011}{x^2}\)
đặt \(\frac{1}{x}\)= y ta có
A= 1- 2y + 2011y^2
cách 1 :
A = 2011y^2 - 2y + 1
= 2011 ( y^2 - \(\frac{2}{2011}y\)+ \(\frac{1}{2011}\))
= 2011( y^2 - 2.y.\(\frac{1}{2011}\)+ \(\frac{1}{2011^2}\)- \(\frac{1}{2011^2}\) + \(\frac{1}{2011}\))
= 2011 \(\left(\left(y-\frac{1}{2011}\right)^2\right)+\frac{2010}{2011^2}\)
= 2011\(\left(y-\frac{1}{2011}\right)^2\)+ \(\frac{2010}{2011}\)
vì ( y - \(\frac{1}{2011}\)) 2>=0
=> 2011\(\left(y-\frac{1}{2011}\right)^2\)+ \(\frac{2010}{2011}\)> = \(\frac{2010}{2011}\)
hay A >=\(\frac{2010}{2011}\)
cách 2
A = 2011y^2 - 2y + 1
= ( \(\sqrt{2011y^2}\)) - 2 . \(\sqrt{2011y}\). \(\frac{1}{\sqrt{2011}}\)+ \(\frac{1}{2011}\)+ \(\frac{2010}{2011}\)
= \(\left(\sqrt{2011y}-\frac{1}{\sqrt{2011}}\right)^2\)+ \(\frac{2010}{2011}\)
vì \(\left(\sqrt{2011y}-\frac{1}{\sqrt{2011}}\right)^2\)> =0
nên \(\left(\sqrt{2011y}-\frac{1}{\sqrt{2011}}\right)^2\)+ \(\frac{2010}{2011}\)>= \(\frac{2010}{2011}\)
hay A >= \(\frac{2010}{2011}\)
12 tháng 4 2018
Ta có :
\(x^2-4x+5=\left(x^2-2.2x+2^2\right)+1=\left(x-2\right)^2+1\ge1>0\)
Vậy đa thức \(x^2-4x+5\) vô nghiệm với mọi giá trị của x
Chúc bạn học tốt ~
CM
2 tháng 7 2019
Điều kiện x ≠ 2 và x ≠ 0
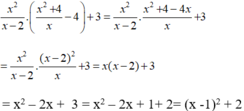
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.
27 tháng 12 2021
Bài 1:
\(A=x^2+6x+9+x^2-10x+25\)
\(=2x^2+4x+34\)
\(=2\left(x^2+2x+17\right)\)
\(=2\left(x+1\right)^2+32>=32\forall x\)
Dấu '=' xảy ra khi x=-1
2D
1
XO
20 tháng 1 2023
B = x2 + 9y2 + 2011
= x2 + (3y)2 + 2011
= x2 + (5 - 2x)2 + 2011 (do 2x + 3y = 5)
= x2 + 4x2 - 20x + 25 + 2011
= 5x2 - 20x + 2036
= 5x2 - 20x + 20 + 2016
= 5(x2 - 4x + 4) + 2016
= 5(x - 2)2 + 2016 \(\ge2016\)
=> Min B = 2016 khi x - 2 = 0 <=> x = 2
khi đó y = \(\dfrac{1}{3}\)
Vậy Bmin = 2016 khi x = 2 ; \(y=\dfrac{1}{3}\)
17 tháng 12 2023
Bài 1:
a: \(M=x^2-10x+3\)
\(=x^2-10x+25-22\)
\(=\left(x^2-10x+25\right)-22\)
\(=\left(x-5\right)^2-22>=-22\forall x\)
Dấu '=' xảy ra khi x-5=0
=>x=5
b: \(N=x^2-x+2\)
\(=x^2-x+\dfrac{1}{4}+\dfrac{7}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>=\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x-1/2=0
=>x=1/2
c: \(P=3x^2-12x\)
\(=3\left(x^2-4x\right)\)
\(=3\left(x^2-4x+4-4\right)\)
\(=3\left(x-2\right)^2-12>=-12\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
Ghi lại đề cho đúng đi bạn.
Sửa đề :
Tìm GTNN của \(A=\frac{x^2-2x+2011}{x^2}\)
Giải :
\(A=\frac{x^2-2x+2011}{x^2}\)
\(A=\frac{x^2}{x^2}-\frac{2x}{x^2}+\frac{2011}{x^2}\)
\(A=1-\frac{2}{x}+\frac{2011}{x^2}\)
\(A=1-2\cdot\frac{1}{x}+2011\cdot\left(\frac{1}{x}\right)^2\)
Đặt \(\frac{1}{x}=a\)
\(A=1-2a+2011a^2\)
\(A=2011\left(a^2-\frac{2}{2011}a+\frac{1}{2011}\right)\)
\(A=2011\left(a^2-2\cdot a\cdot\frac{1}{2011}+\frac{1}{2011^2}+\frac{2010}{4044121}\right)\)
\(A=2011\left[\left(a-\frac{1}{2011}\right)^2+\frac{2010}{4044121}\right]\)
\(A=2011\left(a-\frac{1}{2011}\right)^2+\frac{2010}{2011}\ge\frac{2010}{2011}\forall a\)
Dấu "=" xảy ra \(\Leftrightarrow a=\frac{1}{2011}\)
Thay a ta có : \(\frac{1}{x}=\frac{1}{2011}\)
\(\Rightarrow x=2011\)
Vậy \(A_{min}=\frac{2010}{2011}\Leftrightarrow x=2011\)