K
Khách

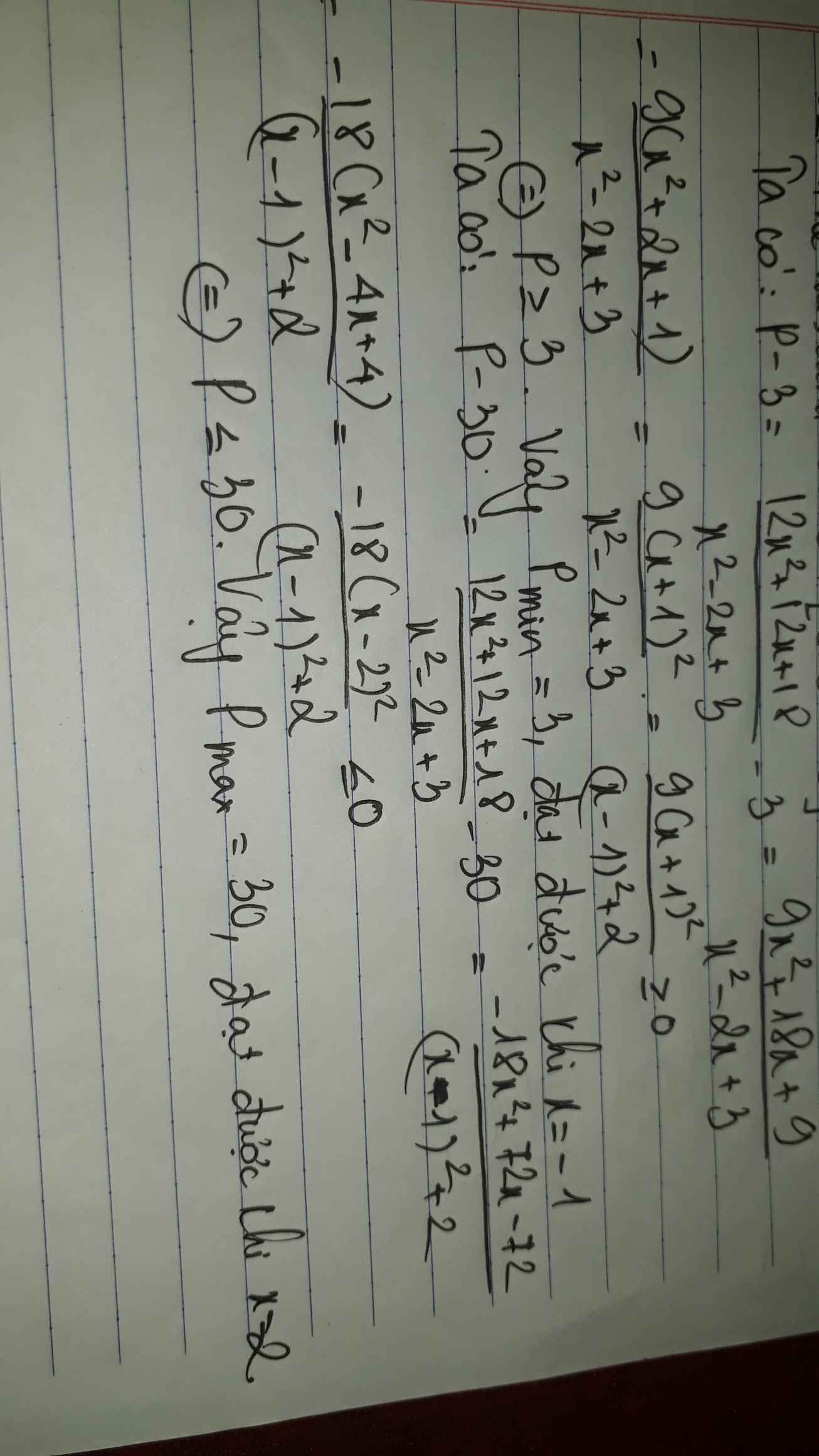
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
NK
Nguyễn Khánh Phương
24 tháng 8 2021
Bài 1: Rút gọn biểu thức D = \(\sqrt{16x^4}-2x^2+1\)Bài 2: Tìm giá trị lớn nhất – nhỏ nhất của biểu thức sau : “ Dùng điều kiện xác định”e) E = \(\dfrac{2\sqrt{x}}{\sqrt{x}+3}\) ĐKXĐ: \(x\ge0\)Bài 3: Tìm giá trị lớn nhất – nhỏ nhất của biểu thức sau : “ Dùng hằng đẳng thức ”B = \(1-\sqrt{x^2-2x+2}\)Bài 4: Cho P = \(\dfrac{4\sqrt{x}+10}{2\sqrt{x}-1}\left(x\ge0;x\ne\dfrac{1}{4}\right)\). Tính tổng các giá trị x nguyên để biểu thức P...
Đọc tiếp

Bài 1: Rút gọn biểu thức D = \(\sqrt{16x^4}-2x^2+1\)

Bài 2: Tìm giá trị lớn nhất – nhỏ nhất của biểu thức sau : “ Dùng điều kiện xác định”

e) E = \(\dfrac{2\sqrt{x}}{\sqrt{x}+3}\) ĐKXĐ: \(x\ge0\)

Bài 3: Tìm giá trị lớn nhất – nhỏ nhất của biểu thức sau : “ Dùng hằng đẳng thức ”

B = \(1-\sqrt{x^2-2x+2}\)

Bài 4: Cho P = \(\dfrac{4\sqrt{x}+10}{2\sqrt{x}-1}\left(x\ge0;x\ne\dfrac{1}{4}\right)\). Tính tổng các giá trị x nguyên để biểu thức P có giá trị nguyên
#Toán lớp 9
1
NL
Nguyễn Lê Phước Thịnh
24 tháng 8 2021

Bài 1: 

Ta có: \(D=\sqrt{16x^4}-2x^2+1\)

\(=4x^2-2x^2+1\)

\(=2x^2+1\)

Đúng(0)
PT
Pham Trong Bach
3 tháng 10 2017

Tìm giá trị nhỏ nhất của biểu thức:

B = 1 2 x - x - 3

#Toán lớp 9
1
CM
Cao Minh Tâm
3 tháng 10 2017

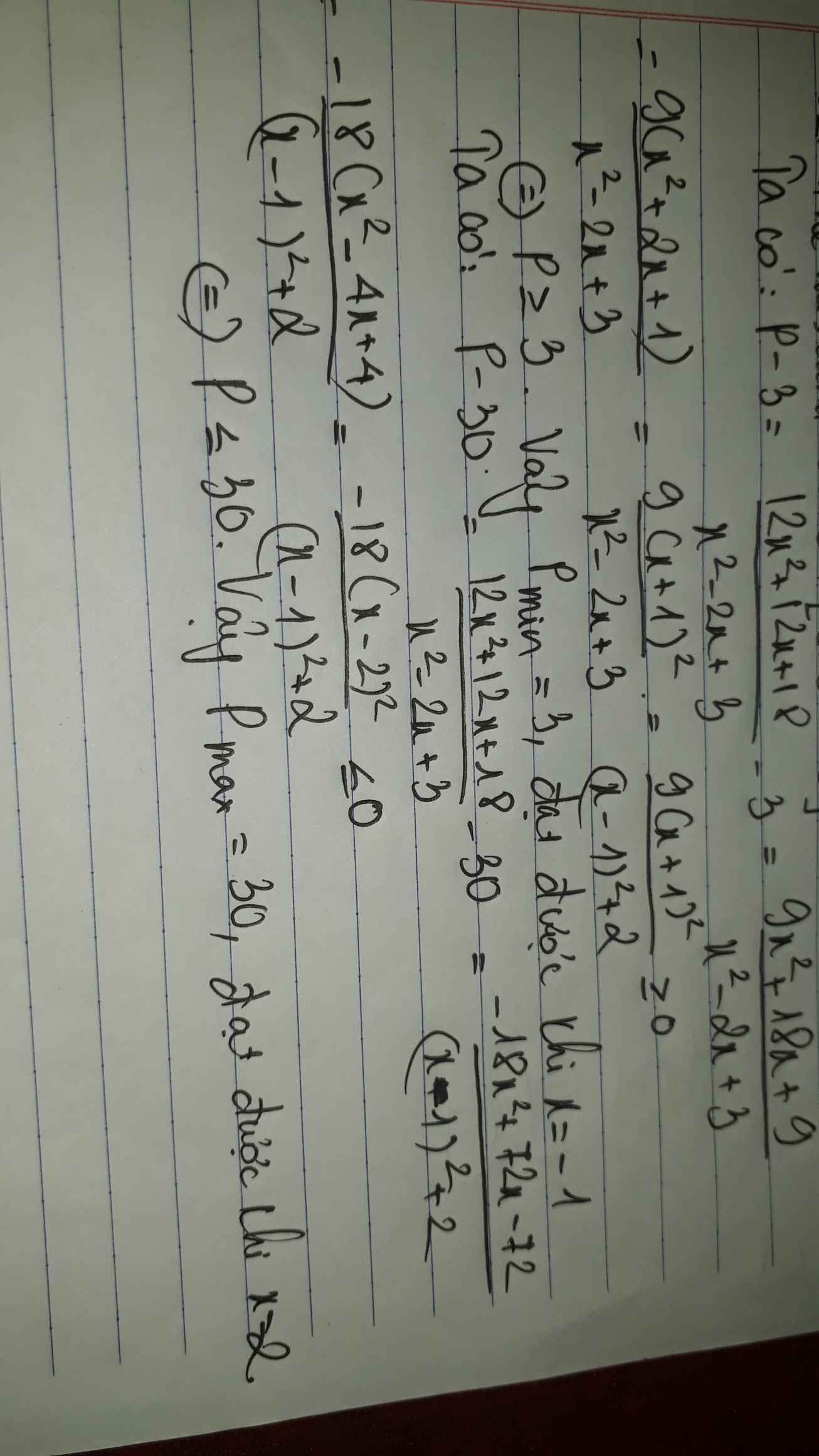
B = 1 2 x - x - 3 ĐK: x>0

2 x - x - 3 = - x - 2 x + 3 = - x - 2 x + 1 + 2 = - x - 1 2 + 2 = - x - 1 2 - 2

Ta có: 

- x - 1 2 ≤ 0 ⇒ - x - 1 2 - 2 ≤ - 2 ⇒ 1 - x - 1 2 - 2 ≥ 1 - 2 ⇒ B ≥ - 1 2

Đúng(0)
HD
Hoàng Đình Đại
10 tháng 2 2020 - olm

Tìm giá trị nhỏ nhất của biểu thức sau:

\(C=x^4-6x^3+11x^2+12x+20\)
#Toán lớp 9
0
PB
Pose Black
21 tháng 7 2023

Bài 8. Tìm giá trị nhỏ nhất của biểu thức: A = \(\sqrt{1-6x+9x^2}\)+ \(\sqrt{9x^2-12x+4}\)
#Toán lớp 9
1
H9
HT.Phong (9A5)
CTVHS
21 tháng 7 2023

\(A=\sqrt{1-6x+9x^2}+\sqrt{9x^2-12x+4}\)

\(A=\sqrt{1^2-2\cdot3x\cdot1+\left(3x\right)^2}+\sqrt{\left(3x\right)^2-2\cdot2\cdot3x+2^2}\)

\(A=\sqrt{\left(1-3x\right)^2}+\sqrt{\left(3x-2\right)^2}\)

\(A=\left|1-3x\right|+\left|3x-2\right|\)

\(A=\left|1-3x+3x-2\right|\)

\(A=\left|-1\right|=1\)

Dấu "=" xảy ra \(\left(1-3x\right)\left(3x-2\right)\ge0\)

\(\Rightarrow\dfrac{1}{3}\le x\le\dfrac{2}{3}\)

Vậy: \(A_{min}=1\) khi \(\dfrac{1}{3}\le x\le\dfrac{2}{3}\)

Đúng(2)
H9
HT.Phong (9A5)
CTVHS
21 tháng 7 2023
Đúng(0)
PI
Play Io Games Nigga
26 tháng 5 2022

1. Giải các phương trình sau
căn x^2-2x+1 + căn x^2-4x+4 = 3
2. Tìm giá trị nhỏ nhất của các biểu thức sau
a, P= (căn 4x^2-4x+1) + (căn 4x^2-12x+9)
b, Q= (căn 49x^2-42x+9) + (căn 49x^2+42x+9)
#Toán lớp 9
1
NL
Nguyễn Lê Phước Thịnh
27 tháng 5 2022

Câu 1: 

\(\sqrt{x^2-2x+1}+\sqrt{x^2-4x+4}=3\)

\(\Leftrightarrow\left|x-1\right|+\left|x-2\right|=3\)(1)

Trường hợp 1: x<1

(1) trở thành 1-x+2-x=3

=>3-2x=3

=>x=0(nhận)

Trường hợp 2: 1<=x<2

(1) trở thành x-1+2-x=3

=>1=3(loại)

Trường hợp 3: x>=2

(1) trở thành x-1+x-2=3

=>2x-3=3

=>2x=6

hay x=3(nhận)

Đúng(2)
LB
Lê Bảo Châu
6 tháng 11 2021

Tìm giá trị nhỏ nhất của biểu thức A=\(\dfrac{2x^2+3}{\sqrt{x^2+4}+2}\)
#Toán lớp 9
1
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 11 2021

Đặt \(\sqrt{x^2+4}=a\ge2\)

\(\Rightarrow x^2=a^2-4\)

\(\Rightarrow A=\dfrac{2\left(a^2-4\right)+3}{a+2}=\dfrac{2a^2-5}{a+2}=2a-4+\dfrac{3}{a+2}\)

\(A=\dfrac{3\left(a+2\right)}{16}+\dfrac{3}{a+2}+\dfrac{29}{16}a-\dfrac{35}{8}\ge2\sqrt{\dfrac{9\left(a+2\right)}{16\left(a+2\right)}}+\dfrac{29}{16}.2-\dfrac{35}{8}=\dfrac{3}{4}\)

\(A_{min}=\dfrac{3}{4}\) khi \(a=2\Rightarrow x=0\)

Đúng(1)
DT
dũng trần
17 tháng 10 2023

e nghĩ mãi khum ra, e c.ơn ạ

Đúng(0)
TD
Trần Đức Huy
7 tháng 2 2022

Cần gấp !!!

Cho \(\sqrt{x+2020}+x^3=\sqrt{y+2020}+y^3\) Tìm giá trị lớn nhất \(P=2x^2-5y^2+xy+12x+2003\)
#Toán lớp 9
1
C
☆Châuuu~~~(๑╹ω╹๑ )☆
7 tháng 2 2022

undefined

Đúng(1)
TD
Trần Đức Huy
7 tháng 2 2022

Châu lớp 8 mà cũng được phết nhỉ

Đúng(0)
TP
Thủy Phạm Thanh
27 tháng 11 2017 - olm

Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức

\(A=\frac{3x^2-2x+3}{x^2+1}\)
#Toán lớp 9
1
DD
Đinh Đức Hùng
27 tháng 11 2017

GTNN :\(A=\frac{\left(2x^2+2\right)+\left(x^2-2x+1\right)}{x^2+1}=2+\frac{\left(x-1\right)^2}{x^2+1}\ge2\forall x\) có GTNN là 2

GTLN : \(A=\frac{\left(4x^2+4\right)-\left(x^2+2x+1\right)}{x^2+1}=4-\frac{\left(x+1\right)^2}{x^2+1}\le4\forall x\) có GTLN là 4

Đúng(0)
TA
Trần Anh Hoàng
12 tháng 1 2023

\(\text{Cho 3 số dương x, y, z thỏa mãn x+y+z=2 tìm giá trị nhỏ nhất của biểu thức A =}\dfrac{2}{x}+\dfrac{8}{9y}+\dfrac{18}{25z}\)
#Toán lớp 9
1
AH
Akai Haruma
Giáo viên
12 tháng 1 2023

Lời giải:
Áp dụng BĐT Bunhiacopxky:
\(\left(\frac{2}{x}+\frac{8}{9y}+\frac{18}{25z}\right)(x+y+z)\geq (\sqrt{2}+\sqrt{\frac{8}{9}}+\sqrt{\frac{18}{25}})^2\)

$\Leftrightarrow A.2\geq \frac{2312}{225}$

$\Leftrightarrow A\geq \frac{1156}{225}$

Vậy $A_{\min}=\frac{1156}{225}$

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP