Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình x2 + 2(m – 1)x + m2 = 0
Có a = 1; b = 2(m – 1); c = m2 nên b’ = m-1
⇒ Δ’ = b'2 – ac = (m – 1)2 – m2 = - 2m + 1.
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ - 2m + 1 ≥ 0 ⇔ m ≤ 1/2.
Khi đó, theo định lý Vi-et: 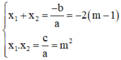
Vậy với m ≤ ½, phương trình có hai nghiệm có tổng bằng -2(m – 1), tích bằng m2

a) Để phương trình có 2 nghiệm phân biệt
<=> \(\Delta=\left[-\left(4m+3\right)^2\right]-4.2.\left(2m-1\right)=16m^2+24m+9-16m+8=16m^2+8m+1+16=\left(4m+1\right)^2+16>0\)
với mọi giá trị của m.
Vậy phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m.
b) Vì phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m nên ta có: x1+x2= \(\dfrac{4m+3}{2}\)và x1.x2=\(\dfrac{2m-1}{2}\)

a) Phương trình x2– 2x + m = 0 có nghiệm khi ∆' = 1 - m ≥ 0 hay khi m ≤ 1
Khi đó x1 + x2 = 2, x1 . x2 = m
b) Phương trình x2 – 2(m – 1)x + m2 = 0 có nghiệm khi
\(\text{∆}'=m^2-2m+1-m^2=1-2m\ge0\)' hay khi m \(\le\dfrac{1}{2}\)
Khi đó x1 + x2 = -2(m – 1), x1 . x2 = m2
a) Phương trình x2– 2x + m = 0 có nghiệm khi ∆' = 1 - m ≥ 0 hay khi m ≤ 1
Khi đó x1 + x2 = 2, x1 . x2 = m
b) Phương trình x2 – 2(m – 1)x + m2 = 0 có nghiệm khi
∆' = m2 - 2m + 1 – m2 = 1 – 2m ≥ 0 hay khi m ≤
Khi đó x1 + x2 = -2(m – 1), x1 . x2 = m2

a) Thay \(x=0\) vào phương trình ta có:
\(\left(m-1\right).0^2-2m.0+m+1=0.\\ \Leftrightarrow m+1=0.\\ \Leftrightarrow m=-1.\)
b) Ta có: \(\Delta'=m^2-\left(m-1\right)\left(m+1\right).\)
\(\Delta'=m^2-\left(m^2-1\right).\\ =m^2-m^2+1.\\ =1>0.\)
\(\Rightarrow\) Phương trình có 2 nghiệm phân biệt \(x_1;x_2.\)
Theo Viet: \(\left\{{}\begin{matrix}x_1.x_2=\dfrac{m+1}{m-1}.\\x_1+x_2=\dfrac{2m}{m-1}.\left(1\right)\end{matrix}\right.\)
Theo đề bài: \(x_1.x_2=5.\)
\(\Rightarrow\dfrac{m+1}{m-1}=5.\\ \Leftrightarrow m+1=5m-5.\\ \Leftrightarrow4m-6=0.\\ \Leftrightarrow m=\dfrac{3}{2}.\)
Thay \(m=\dfrac{3}{2}\) vào \(\left(1\right):\)
\(x_1+x_2=\) \(\dfrac{2.\dfrac{3}{2}}{\dfrac{3}{2}-1}=\dfrac{3}{\dfrac{1}{2}}=6.\)

a) x = 0 là nghiệm của phương trình
=> (m-1).02 -2.m.0 + m + 1 = 0
<=> m + 1 = 0 <=> m = -1
vậy m = -1 thì pt có nghiệm là x = 0
b) PT có 2 nghiệm thì trước hết pt đã cho là phương trình bậc 2 <=> m - 1\(\ne\) 0 <=> m \(\ne\)1
\(\Delta\)' = (-m)2 - (m - 1)(m +1) = m2 - (m2 - 1) = 1 > 0
=> phương trình đã cho có 2 nghiệm là:
x1 = \(\frac{m+1}{m-1}\) ; x2 = \(\frac{m-1}{m-1}\) = 1
+) Để x1 .x2 = 5 <=> \(\frac{m+1}{m-1}\) = 5 <=> m +1 = 5( m - 1)
<=> m +1 = 5m - 5
<=> 6 = 4m <=> m = 3/2 (Thoả mãn)
+) Khi đó x1 + x2 = \(\frac{m+1}{m-1}\) + 1 = \(\frac{m+1+m-1}{m-1}=\frac{2m}{m-1}=\frac{2.\frac{3}{2}}{\frac{3}{2}-1}=\frac{3}{\frac{1}{2}}=6\)
Mình không đồng ý với phần tìm đen-ta của bạn Trần Thị Loan
Phương trình (m-1)x2 - 2mx + m + 1 = 0 ( a=m-1; b=-2m; c=m+1)
đen-ta = (-2m)2 - 4.(m-1).(m=1)=4
Vì đen-ta = 4 > 0 nên phương trình có 2 nghiệm phân biệt với mọi m

Bài 1 : a, Thay m = -2 vào phương trình ta được :
\(x^2+8x+4+6+5=0\Leftrightarrow x^2+8x+15=0\)
Ta có : \(\Delta=64-60=4>0\)
Vậy phương trình có 2 nghiệm phân biệt
\(x_1=\frac{-8-2}{2}=-5;x_2=\frac{-8+2}{2}=-3\)
b, Đặt \(f\left(x\right)=x^2-2\left(m-2\right)x+m^2-3m+5=0\)
\(f\left(-1\right)=\left(-1\right)^2-2\left(m-2\right)\left(-1\right)+m^2-3m+5=0\)
\(1+2\left(m-2\right)+m^2-3m+5=0\)
\(6+2m-4+m^2-3m=0\)
\(2-m+m^2=0\)( giải delta nhé )
\(\Delta=\left(-1\right)^2-4.2=1-8< 0\)
Vậy phương trình vô nghiệm
c, Để phương trình có nghiệm kép \(\Delta=0\)( tự giải :v )
a) Phương trình x 2 − 2 x + m = 0
Có a = 1; b = -2; c = m nên b’= -1
⇒ Δ ' = ( − 1 ) 2 − 1 ⋅ m = 1 − m
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ 1 – m ≥ 0 ⇔ m ≤ 1.
Khi đó, theo định lý Vi-et: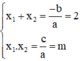
Vậy với m ≤ 1, phương trình có hai nghiệm có tổng bằng 2; tích bằng m.
b) Phương trình
x 2 + 2 ( m − 1 ) x + m 2 = 0 C ó ( a = 1 ; b = 2 ( m − 1 ) c = m 2 nên b ' = m − 1 ⇒ Δ ' = b ' 2 − a c = ( m − 1 ) 2 − m 2 = − 2 m + 1
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ - 2m + 1 ≥ 0 ⇔ m ≤ 1/2.
Khi đó, theo định lý Vi-et: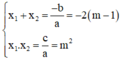
Vậy với m ≤ ½, phương trình có hai nghiệm có tổng bằng -2(m – 1), tích bằng m 2