Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐKXĐ:
a.
\(x^2-9\ge0\Rightarrow\left[{}\begin{matrix}x\ge3\\x\le-3\end{matrix}\right.\)
b.
\(\left(3x+2\right)\left(x-1\right)\ge0\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le-\dfrac{2}{3}\end{matrix}\right.\)
c.
\(\left\{{}\begin{matrix}3x-2\ge0\\x-1\ge0\end{matrix}\right.\) \(\Rightarrow x\ge1\)
a) x khác 0, khác 3
b) x khác 0, khác 1, khác 2/3
c) x khác 0, khác 1, khác 2/3

Câu b bạn có bị lỗi dấu căn không mà sao nó kéo dài cả 2 vế pt vậy :v
\(a,\sqrt{x^2-6x+9}+x=11\\ \Leftrightarrow\sqrt{\left(x-3\right)^2}=11-x\)
\(\Leftrightarrow\left|x-3\right|=11-x\\ TH_1:x\ge3\\ x-3=11-x\\ \Leftrightarrow2x=14\\ \Leftrightarrow x=7\left(tm\right)\)
\(TH_2:x< 3\\ -x+3=11-x\\ \Leftrightarrow-x+x=11-3\\ \Leftrightarrow0=8\left(VL\right)\)
Vậy \(S=\left\{7\right\}\)
\(c,\sqrt{16\left(x+1\right)}-\sqrt{9\left(x+1\right)}=4\) \(\left(dk:x\ge-1\right)\)
\(\Leftrightarrow\sqrt{4^2}.\sqrt{\left(x+1\right)}-\sqrt{3^2}.\sqrt{\left(x+1\right)}=4\left(1\right)\)
Đặt \(a=\sqrt{x+1}\left(a\ge0\right)\)
Pt trở thành : \(4a-3a=4\Leftrightarrow a=4\left(tmdk\right)\)
\(\Rightarrow\sqrt{x+1}=4\\ \Rightarrow\left(\sqrt{x+1}\right)^2=16\\ \Rightarrow\left|x+1\right|=16\)
\(TH_1:x\ge-1\\ x+1=16\Leftrightarrow x=15\left(tm\right)\\ TH_2:x< -1\\ -x-1=16\Leftrightarrow x=-17\left(tm\right)\)
Nhưng loại TH2 vì dk ban đầu là \(x\ge-1\)
Vậy \(S=\left\{15\right\}\)
\(d,\sqrt{9x+9}+\sqrt{4x+4}=\sqrt{x+1}\left(dk:x\ge-1\right)\\ \Leftrightarrow\sqrt{9}.\sqrt{x+1}+\sqrt{4}.\sqrt{x+1}-\sqrt{x+1}=0\)
Đặt \(\sqrt{x+1}=a\left(a\ge0\right)\)
Tới đây bạn làm tương tự câu c nha.

a, ĐKXĐ : \(x\ge\dfrac{1}{2}\)
PT <=> 2x - 1 = 5
<=> x = 3 ( TM )
Vậy ...
b, ĐKXĐ : \(x\ge5\)
PT <=> x - 5 = 9
<=> x = 14 ( TM )
Vậy ...
c, PT <=> \(\left|2x+1\right|=6\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=6\\2x+1=-6\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)
Vậy ...
d, PT<=> \(\left|x-3\right|=3-x\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=x-3\\x-3=3-x\end{matrix}\right.\)
Vậy phương trình có vô số nghiệm với mọi x \(x\le3\)
e, ĐKXĐ : \(-\dfrac{5}{2}\le x\le1\)
PT <=> 2x + 5 = 1 - x
<=> 3x = -4
<=> \(x=-\dfrac{4}{3}\left(TM\right)\)
Vậy ...
f ĐKXĐ : \(\left[{}\begin{matrix}x\le0\\1\le x\le3\end{matrix}\right.\)
PT <=> \(x^2-x=3-x\)
\(\Leftrightarrow x=\pm\sqrt{3}\) ( TM )
Vậy ...
a) \(\sqrt{2x-1}=\sqrt{5}\) (x \(\ge\dfrac{1}{2}\))
<=> 2x - 1 = 5
<=> x = 3 (tmđk)
Vậy S = \(\left\{3\right\}\)
b) \(\sqrt{x-5}=3\) (x\(\ge5\))
<=> x - 5 = 9
<=> x = 4 (ko tmđk)
Vậy x \(\in\varnothing\)
c) \(\sqrt{4x^2+4x+1}=6\) (x \(\in R\))
<=> \(\sqrt{\left(2x+1\right)^2}=6\)
<=> |2x + 1| = 6
<=> \(\left[{}\begin{matrix}\text{2x + 1=6}\\\text{2x + 1}=-6\end{matrix}\right.< =>\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=\dfrac{-7}{2}\end{matrix}\right.\)(tmđk)
Vậy S = \(\left\{\dfrac{5}{2};\dfrac{-7}{2}\right\}\)

a: ĐKXĐ; 2011-m>=0
=>m<=2011
b: ĐKXĐ: (2căn 15-căn 59)/(x-7)>=0
=>x-7>0
=>x>7
c: ĐKXĐ: 4x^2+4x+1>=0
=>(2x+1)^2>=0(luôn đúng với mọi x)
d: ĐKXĐ: 12x+5>=0
=>x>=-5/12
`a, Đk: 2011-m>=0 <=> m <=2011.`
`b, Đk: x-7>0 <=> x > 7`
`c, Đk: x in RR`.
`d, Đk: 12x + 5 >=0 <=> x >=-5/12`

`a)ĐKXĐ:{(x > 0),(x \ne 4):}`
`b)` Với `x > 0,x \ne 4` có:
`A=[\sqrt{x}(\sqrt{x}+2)+\sqrt{x}(\sqrt{x}-2)]/[x-4].[x-4]/[\sqrt{4x}]`
`A=[x-2\sqrt{x}+x-2\sqrt{x}]/[2\sqrt{x}]`
`A=[2\sqrt{x}(\sqrt{x}-2)]/[2\sqrt{x}]=\sqrt{x}-2`
`c)` Với `x > 0,x \ne 4` có:
`A < 3 <=>\sqrt{x}-2 < 3<=>\sqrt{x} < 5<=>x < 25`
Kết hợp đk
`=>0 < x < 25 ,x \ne 4`

a) A xác định khi:
x - 3 ≥ 0 và 4 - x > 0
⇔ x ≥ 3 và x < 4
⇔ 3 ≤ x < 4
b) B xác định khi x - 1 > 0 và x - 2 ≠ 0
⇔ x > 1 và x ≠ 2
a) \(A=\sqrt[]{x-3}-\sqrt[]{\dfrac{1}{4-x}}\left(1\right)\)
\(\left(1\right)xđ\Leftrightarrow\left\{{}\begin{matrix}x-3\ge0\\4-x>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge3\\x< 4\end{matrix}\right.\)
\(\Leftrightarrow3\le x< 4\)
b) \(B=\dfrac{1}{\sqrt[]{x-1}}+\dfrac{2}{\sqrt[]{x^2-4x+4}}\left(1\right)\)
\(\left(1\right)xđ\Leftrightarrow\left\{{}\begin{matrix}x-1>0\\x^2-4x+4>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>1\\\left(x-2\right)^2>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>1\\x\ne2\end{matrix}\right.\)
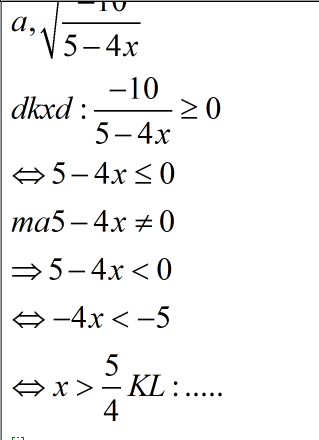
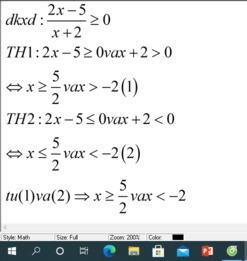
a) ĐKXĐ: 4x ≥ 0 ⇔ x ≥ 0
b) ĐKXĐ: 5.(-x) ≥ 0 ⇔ -x ≥ 0 ⇔ x ≤ 0
c) ĐKXĐ: 4 - x² ≥ 0 ⇔ x² ≤ 4 ⇔ -2 ≤ x ≤ 2
d) 4x² - 1 ≥ 0 ⇔ 4x² ≥ 1 ⇔ x² ≥ 1/4 ⇔ -1/2 ≤ x hoặc x ≥ 1/2