
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: (3x-5)2006 lớn hơn hoặc = 0 với mọi x
(y2-1)2008 lớn hơn hoặc = 0 vs moi y
(x-z)2100 lớn hơn hoặc = 0 vs mọi x, z
=> (3x-5)2006+(y2-1)2008+(x-z)2100 lớn hơn howacj = 0 vs mọi x
mà (3x-5)2006+(y2-1)2008+(x-z)2100=0
=> (3x-5)2006=0 ; (y2-1)2008=0 và (x-z)2100=0
+) xét (3x-5)2006=0
=>3x-5=0
=>3x=5
=>x=5/3
+) xét (y2-1)2008=0
=>y2-1=0
=>y2=1
=>y=-1 hoặc y=1
+) xét (x-z)2100=0
=>x-z=0
=>5/3-z=0
=>z=5/3

Ta có: \(\left(3x-5\right)^{2006}\ge0\)với mọi x
\(\left(y^2-1\right)^{2008}\ge0\)với mọi y
\(\left(x-z\right)^{2100}\ge0\) với mọi x,z
\(\Rightarrow\)\(\left(3x-5\right)^{2006}+\left(y^2-1\right)^{2008}+\left(x-z\right)^{2100}\ge0\)với mọi x
Mà \(\left(3x-5\right)^{2006}+\left(y^2-1\right)^{2008}+\left(x-z\right)^{2100}=0\)
\(\Rightarrow\left(3x-5\right)^{2006}=0;\left(y^2-1\right)^{2008}=0;\left(x-y\right)^{2100}=0\)
Xét:
\(\left(3x-5\right)^{2006}=0\hept{\begin{cases}3x-5=0\\3x=5\\x=\frac{5}{3}\end{cases}}\)
Xét:
\(\left(y^2-1\right)^{2008}=0\hept{\begin{cases}y^2-1=0\\y^2=1\\y=1hoac-1\end{cases}}\)
Xét:
\(\left(x-z\right)^{2100}=0\hept{\begin{cases}x-z=0\\\frac{5}{3}-z=0\\z=\frac{5}{3}\end{cases}}\)
\(\left(3x-5\right)^{2006}+\left(y^2-1\right)^{2008}+\left(x-z\right)^{2100}=0\)
\(\left(3x-5\right)^{2006}+\left(y^2-1\right)^{2008}+\left(x-z\right)^{2100}=0\)
\(\left(3x-5\right)^{2006}+\left(y^2-1\right)^{2008}+\left(x-z\right)^{2100}=0\)
\(\Leftrightarrow\hept{\begin{cases}3x-5=0\\y^2-1=0\\x-z=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=z=\frac{5}{3}\\y=1\end{cases}}\)

Ta có:
\(\left(3x-5\right)^{2006}+\left(y^2-1\right)^{2008}+\left(x-z\right)^{2100}=0\)
Vì \(\left\{{}\begin{matrix}\left(3x-5\right)^{2006}\ge0\\\left(y^2-1\right)^{2008}\ge0\\\left(x-z\right)^{2100}\ge0\end{matrix}\right.\)
\(\Rightarrow\left(3x-5\right)^{2006}+\left(y^2-1\right)^{2008}+\left(x-z\right)^{2100}=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(3x-5\right)^{2006}=0\\\left(y^2-1\right)^{2008}=0\\\left(x-z\right)^{2100}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-5=0\\y^2-1=0\\x-z=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{3}\\y=\pm1\\z=\dfrac{5}{3}\end{matrix}\right.\)
Vậy ...
Chúc bạn học tốt!

=>3x-5=0 và y2-1=0 và x-z=0
=>x=5/3 và y=-1 hoặc y=1 và z=5/3

c) TH1 : x <=3 thì |3 -x| = 3 -x do đó ta đc 3 - x + 3x - 1 =0=> x = -1
TH2 : x > 3 thì |3 -x| = x -3, do đó ta đc : x - 3 + 3x -1 =0 => x = 1
a, Xét (3x-5)^2006; (y^2-1)^2008;9x-7)^2100 lú nào cũng lớn hơn hoặc bằng 0 nên suy ra (3x-5)^2006 +(Y^2-1)^2008+(x-7)^2100 >hoặc bằng 0 . Dể cộng vào bằng 0 thì (3x-5)^2006 =0; (y^2-1)^2008=0; (x-7)^2100=0 suy ra 3x-5=0;Y^2-1=0;'x-7=0
3x=5,x=5/3; y^2=1 ,y=+ - 1;x=7

Dễ thấy từng hạng tử đều mang lũy thừa chẵn nên:
\(\Leftrightarrow\hept{\begin{cases}3x-5=0\\y^2-1=0\\x-z=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{3}\\y=1;y=-1\\z=\frac{5}{3}\end{cases}}}\)\(\Rightarrow\left(x;y;z\right)=\left(\frac{5}{3};1;\frac{5}{3}\right),\left(\frac{5}{3};-1;\frac{5}{3}\right)\)

\(\left(3x-5\right)^{2006}\ge0;\left(y^2-1\right)^{2008}\ge0;\left(x-z\right)^{2100}\ge0\) với mọi x,y,z
mà theo đề:......=0
\(\Rightarrow\left(3x-5\right)^{2006}=0\Rightarrow3x-5=0\Rightarrow3x=5\Rightarrow x=\frac{5}{3}\)
\(y^2-1=0\Rightarrow y^2=1\Rightarrow y\in\left\{-1;1\right\}\)
\(\left(x-z\right)^{2100}=0\Rightarrow x-z=0\Rightarrow x=z\Rightarrow z=\frac{5}{3}\)
vậy...

\(2a=3b\Rightarrow\dfrac{a}{3}=\dfrac{b}{2}\Rightarrow\dfrac{a}{21}=\dfrac{b}{14}\\ 5b=7c\Rightarrow\dfrac{b}{7}=\dfrac{c}{5}\Rightarrow\dfrac{b}{14}=\dfrac{c}{10}\\ \Rightarrow\dfrac{a}{21}=\dfrac{b}{14}=\dfrac{c}{10}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{21}=\dfrac{b}{14}=\dfrac{c}{10}=\dfrac{3a}{63}=\dfrac{7b}{98}=\dfrac{5c}{50}=\dfrac{3a-7b+5c}{63-98+50}=\dfrac{-30}{15}=-2\\ \Rightarrow\left\{{}\begin{matrix}a=-42\\b=-28\\c=-20\end{matrix}\right.\)
\(x:y:z=3:4:5\Rightarrow\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=k\Rightarrow x=3k;y=4k;z=5k\)
\(2x^2+2y^2-3z^2=-100\\ \Rightarrow18k^2+32k^2-75k^2=-100\\ \Rightarrow-25k^2=-100\Rightarrow k^2=4\Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=6;y=8;z=10\\x=-6;y=-8;z=-10\end{matrix}\right.\)

Cộng theo từng vế các đẳng thức đã cho, ta được:
x.(x + y + z) + y(x + y + z) + z.(x+ y + z) = - 5 + 9 + 5
⇔ (x + y + z). (x + y + z ) = 9
Suy ra: (x + y + z)2 = 9 ⇒ x + y + z = ±3
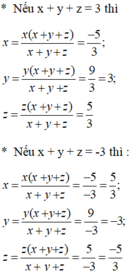
(3\(x\) - 5)2006 + (y - 1)2008 + (\(x\) - 2z)2100 = 0
Vì (3\(x\) - 5)2006 ≥ 0; (y - 1)2008 ≥ 0; (\(x\) - 2z)2100 ≥ 0 ∀ \(x;y;z\)
Vậy (3\(x-5\))2006 + (y - 1)2008 + (\(x\) - 2z)2100 = 0
⇔ \(\left\{{}\begin{matrix}3x-5=0\\y-1=0\\x-2z=0\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}x=\dfrac{5}{3}\\y=1\\z=\dfrac{x}{2}=\dfrac{5}{6}\end{matrix}\right.\)
Vậy...