Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án B
Hoành độ giao điểm của đồ thị hàm số đã cho và trục hoành là nghiệm của phương trình :
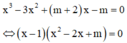
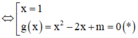
Để đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục hoành
Phương trình (*) có hai nghiệm phân biệt khác 1
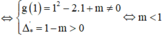
Đáp án C
Phương pháp : Xét từng mệnh đề.
Cách giải:
(I) sai. Ví dụ hàm số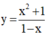 
có đồ thị hàm số như sau:
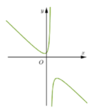õ ràng 
(II) đúng vì y ' = 4 a x 3 + 2 b x = 0 luôn có một nghiệm x = 0 nên đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III) Gọi
x
0
là 1 điểm cực trị của hàm số 
=> Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là: 
luôn song song với trục hoành.
Vậy (III) đúng.
· Đường tròn
C m : x 2 + y 2 - 2 m x - 4 m y + 5 m 2 - 1 = 0
có tâm I ( m;2m ), bán kính R = 1.Ta có:
I B = 5 m 2 + 4 m + 8 = 5 m + 2 5 2 + 36 5 ≥ 6 5 > 1 = R
điểm B nằm ở phía ngoài đường tròn C m . Do đó điểm A nằm ở phía trong đường tròn C m , tức là:
L A < 1 = R ⇔ 5 m 2 - 8 m + 4 < 1 ⇔ 5 m 2 - 8 m + 3 < 0 ⇔ 3 5 < m < 1
Đáp án C
Đáp án D
Điều kiện để hai điểm cực trị nằm về hai phía của trục hoành PT y = 0 có ba nghiệm phân biệt. Xét PT
x 3 + 1 − 2 m x 2 + 2 2 − m x + 4 = 0 ⇔ x 3 + x 2 − 2 m x 2 + 2 m x + 4 x + 4 = 0 ⇔ x + 1 x 2 − 2 m x + 4 = 0
Để PT này có ba nghiệm phân biệt thì
Δ ' = m 2 − 4 > 0 − 1 2 − 2 m . − 1 + 4 ≠ 0 ⇔ m ∈ − ∞ ; − 2 ∪ 2 ; + ∞ m ≠ − 5 2
Đáp án C
TXĐ: D = ℝ .
Ta có y ' = x 2 − 2 m − 1 x + m − 1 .
Để đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục tung thì
m − 1 2 − m − 1 > 0 m − 1 > 0 2 m − 1 > 0 ⇔ m > 2.
Vậy m>2 thỏa mãn điều kiện đề bài.
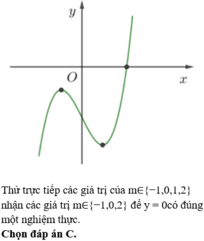
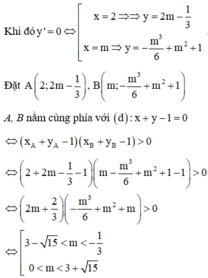
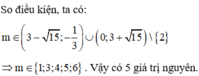
Đáp án C
y ' = x 2 − 6 m x ; y ' = 0 ⇔ x 1 = 0 x 2 = 6 m .
Đồ thị hàm số có điểm cực đại, cực trị ⇔ y ' = 0 có hai nghiệm phân biệt ⇔ m ≠ 0 .
Các điểm cực trị nằm về hai phía của trục hoành ⇔ y 1 y 2 < 0
⇔ m − 36 m 3 + m < 0 ⇔ m 2 − 36 m 2 + 1 < 0 ⇔ m > 1 6 .