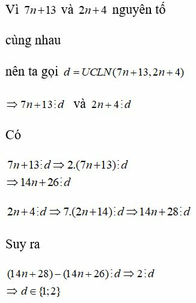K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VH
0
LC
24 tháng 10 2015
Gọi ƯC(7n+13,2n+4)=d
Ta có: 7n+13 chia hết cho d=>2.(7n+13)=14n+26 chia hết cho d
2n+4 chia hết cho d=>7.(2n+4)=14n+28 chia hết cho d
=>14n+28-(14n+26) chia hết cho d
=>2 chia hết cho d
=>d=Ư(2)=(1,2)
Để 7n+13 và 2n+4 là nguyên tố cùng nhau
=>d=1
=>d khác 2
=>7n+13 không chia hết cho 2
=>7n+13 khác 2k
=>7k khác 2k-13
=>k khác (2k-13)/2
PT
1
CM
6 tháng 10 2019
Vì 7n+13 và 2n+4 nguyên tố cùng nhau nên ta gọi d = UCLN(7n+13,2n+4)
=>7n+13 ⋮ d và 2n+4 ⋮ d
Có 7n+13 ⋮ d => 2(7n+13) ⋮ d => 14n+26 ⋮ d
2n+4 ⋮ d => 7.(2n+14) ⋮ d => 14n+28 ⋮ d
Suy ra (14n+28) – (14n+26) ⋮ d => 2 ⋮ d => d ∈ {1;2}
Nếu d = 1 thì 7n+13 và 2n+4 là nguyên tố cùng nhau
Nếu d = 2 => 7n+13 ⋮ 2 => 7.(n+1)+6 ⋮ 2 vì 6 ⋮ 2 nên 7.(n+1) ⋮ 2 mà UC(7,2) = 1 => n+1 ⋮ 2
Để n+1 ⋮ 2 thì n = 2k+1
Vậy để 7n+13 và 2n+4 là số nguyên tố cùng nhau thì n ≠ 2k+1
PT
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
9 tháng 11 2023
a,tim n \(\in\) N; 4n + 3 và 2n + 3 nguyên tố cùng nhau
Gọi ước chung lớn nhất của 4n + 3 và 2n + 3 là d ta có:
\(\left\{{}\begin{matrix}4n+3⋮d\\2n+3⋮d\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}4n+3⋮d\\\left(2n+3\right).2⋮d\end{matrix}\right.\) \(\Rightarrow\) \(\left\{{}\begin{matrix}4n+3⋮d\\4n+6⋮d\end{matrix}\right.\)
⇒ 4n + 6 - (4n + 3) ⋮ d ⇒ 4n + 6 - 4n - 3 ⋮ d ⇒ 3 ⋮ d
⇒ d = 1; 3
Để 4n + 3 và 2n + 3 là hai số nguyên tố cùng nhau thì
2n + 3 không chia hết cho 3
2n không chia hết cho 3
n = 3k + 1; hoặc n = 3k + 2 (k \(\in\) N)
CC
0
NH
1
