K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
cho a và b là 2 số nguyên dương ko chia hết cho nhau. Biết BCNN(a,b)=630 và UCLN(a,b)=18. Tìm a và b
1
22 tháng 4 2016
Theo đề bài ta có : UCLN(a,b)=18
=> a= 18m ; b = 18 n UCLN (m,n) = 1
ta có : a.b= BCNN(a,b).UCLN(a,b)=630.18=5670
=18m.18n=324.m.n=11340
=>m.n=11340:324=35
=>m,n thuộc U(35)={1,5,7,3}lập bảng
| m | n | a | b |
| 1 | 35 | 18 | 630 |
| 5 | 7 | 90 | 126 |
| 7 | 5 | 126 | 90 |
| 35 | 1 | 630 | 18 |
vậy các cặp a,b thỏa mãn là (18,630);(90;126);(126;90);(630;18)
like mình nha
23 tháng 3 2018
Đúng bạn ạ! nhưng bạn quên mất trường hợp là a và b là 2 số nguyên dương ko chua hết cho nhau
NT
3
LM
3 tháng 3 2016
vì a/b=15/35=3/7
=>a:3=b:7
=>a=3/7b
mà ƯCLN(a,b).BCNN(a,b)=a.b
=>3/7b.b=3549
=>b=91, a=3/7b=39
16 tháng 2 2017
Ta có: \(\frac{a}{b}\)= \(\frac{15}{35}\)= \(\frac{3}{7}\).
Suy ra: a= 3K; b= 7K, với k thuộc N*.
Ta có: ƯCLN (a,b)= ƯCLN(3K,7K)= K
LV
1
30 tháng 3 2016
NX: /a+c-42/>= 0 với mọi x
/b+a-22/>= 0 với mọi x
/b+c-40/>= 0 với mọi x
=> /a+c-42/+/b+a-22/+/b+c-40/>= 0 với mọi x
mà theo đề bài /a+c-42/+/b+a-22/+/b+c-40/<hoặc=0
=> /a+c-42/=0
=> a+c=42(1)
/b+a-22/=0
=>a+b=22 (2)
/b+c-40/=0
=>b+c=40 (3)
Từ (1)(2)(3)=> a+b+b+c+a+c=104
=> a+b+c=52(4)
từ(1) và (4)=> b=10
từ(2)và(4)=>c=30
từ(3)và(4)=>a=12
Vậy a=12 ; b=10;c=30
28 tháng 1 2022
Bài 1:
a: \(\Leftrightarrow x\cdot\dfrac{3}{4}=-1\)
hay x=-4/3
b: =>x=4/8+3/7=1/2+3/7=7/14+6/14=13/14
Bài 3:
BCNN(16;32;5)=160
UCLN(16;32;5)=1
1 tháng 4 2016
Từ a - b = 7 hay a = b+7 do đó nếu a chia hết cho 7 thì b cũng chia hết cho 7 và ngược lại. (*)
Lại có BCNN(a,b) = 140 suy ra: a hoặc b chia hết cho 7 (vì 7 là ước của 140). (**)
Từ (*)(**) suy ra a và b đều chia hết cho 7.
Đặt b=7k (k nguyên dương) suy ra a = 7(k+1)
khi đó BCNN(a;b) = BCNN(7(k+1),7k) = 140
hay BCNN(k+1;k) = 20 (chia 2 vế cho 7)
tương đương k(k+1) = 20 (vì UCLN(k+1;k) = 1)
Giải ra k = 4, suy ra b = 28; a = 35
Vậy 2 số phải tìm là: a = 35 và b = 28
CM
11 tháng 2 2018
Đáp án B
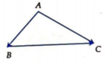
Cách 1:
Đặt A B → = a → ; A C → = b → ⇒ A B → , A C → = B A C ^ = 120 0
Ta có A B → − A C → = B C → = a → − b →
Áp dụng định lý hàm cosin cho tam giác ABC ta có
B C 2 = A B 2 + A C 2 − 2 A B . A C . cos B A C ^ = 49 ⇒ B C = 7
Ta chọn B
Cách 2:
a → − b → 2 = a → 2 + b → 2 − 2 a → b → = a → 2 + b → 2 − 2 a → b → cos a → , b → = 3 2 + 5 2 − 2.3.5. − 1 2 = 49
⇒ a → − b → 2 = 49 ⇒ a → − b → = 7
Ta chọn B
KH
3
24 tháng 11 2017
ƯCLN(a,b)=32. Đặt a= 6x ; b= 6y
với ƯCLN(x,y)=1 và x,y ∈ N
ta có : a.b=216
6x.6y=216
x.y=216:(6.6)
x.y= 6
từ trên ta có bảng:
| x | 1 | 2 | 3 | 6 |
| y | 6 | 3 | 2 | 1 |
do đó, ta có:
a=6.1=6;b=6.6=36
a=6.2=12;b=6.3=18
a=6.3=18;b=6.2=12
a=6.6=36;b=6.1=6
CHÚC BẠN LÀM TỐT NHÉ!
Ta có: \(72=2^3.3^2\)
\(\Rightarrow\) Trong 2 số a, b có một số chia hết cho 2
Giả sử a chia hết cho 2
\(b=\left(42-a\right)\) ⋮ \(2\)
\(\Rightarrow\) a và b ⋮ 2
Tương tự ta cũng có a và b ⋮ 3
\(\Rightarrow\) a và b ⋮ 6
Dễ thấy \(42=36+6=30+12=18+24\) (VÌ tổng 2 số ⋮ 6)
Mà trong ba tổng trên chỉ có \(18+24\) thỏa mãn
\(\Rightarrow a=18;b=24\)