Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

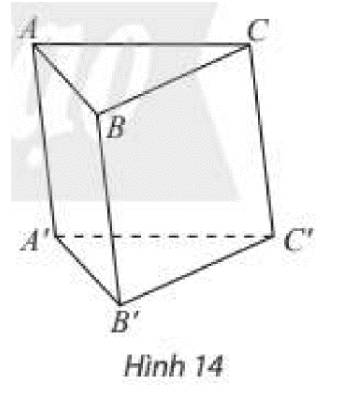
Chúng ta sẽ chia thành 3 khối như sau:
A.A'B'C', B'.ABC và C.A'B'C'
tham khảo:

Ba tứ diện A'.ABC, C.A'B'B, C.A'B'C' có cùng chiều cao và diện tích đáy.

A B C D M N P Q
a/ Trong mp (BCD) dựng đường thẳng // với CD cắt BD tại P => CD//NP (1)
=> mp (MNP) là mp \(\alpha\)
Trong mp (ACD) từ M dựng đường thẳng //CD cắt AC tại Q => CD//MQ (2)
Từ (1) và (2) => NP//MQ => MPNQ là thiết diện của tứ diện ABCD với mp \(\alpha\)
b/
Xét tg ACD có
MQ//CD và MA=MD => QA=QC (trong tam giác đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại của tam giác => MQ là đường trung bình của tg ACD \(\Rightarrow MQ=\frac{CD}{2}\)
Ta có MQ//NP để MPNQ là hình bình hành thì \(MQ=NP=\frac{CD}{2}\) (tứ giác có 1 cặp cạnh đối // và = nhau thì tứ giác là hbh)
=> NP là đường trung bình của tg BCD => N là trung điểm của BC
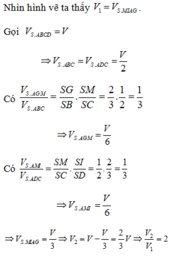


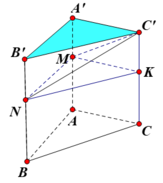
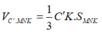

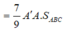



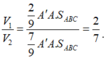
Đáp án C
Có 3 phương án đúng: i, iii, iv.