NT
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
5
PT
6 tháng 4 2016
Gọi 2n là số tự nhiên chẵn thứ nhất (\(n\in |N\))
Ta có, 4 số tự nhiên chẵn liên tiếp là: 2n; 2n+2; 2n+4; 2n+6
Theo đề, ta có: 2n + 2n+2 + 2n+4 + 2n+6 =5420
<=> 4.2n + 12 = 5420
<=> 2n = (5420 - 12)/4
<=> 2n = 1352 (nhận, vì 2n \(\in\) N nên n \(\in\) N)
Vậy 4 số tự nhiên chẵn liên tiếp là: 1352; 1354; 1356; 1358
NT
2
L
16 tháng 2 2016
Đặt tích 2 số tự nhiên liên tiếp là \(a\left(a+1\right)=a^2+a\)
Ta sẽ xét xem tích 2 số tự nhiên liên tiếp chia cho 3 dư bao nhiêu.
TH1: a chia hết cho 3
\(\Rightarrow\)a2 chia hết cho 3 và a cũng chia hết cho 3
\(\Rightarrow a^2+a\) chia hết cho 3
\(\Rightarrow a\left(a+1\right)\) chia hết cho 3
TH2: a chia 3 dư 1 -> a có dạng 3k+1
\(\Rightarrow a^2=\left(3k+1\right)^2=\left(3k+1\right)\left(3k+1\right)=\left(3k+1\right)3k+\left(3k+1\right).1=9k^2+3k+3k+1\)\(=3.\left(3k^2+k+k\right)+1\)
\(\Rightarrow a^2+a=3.\left(3k^2+k+k\right)+1+3k+1=3.\left(3k^2+k+k+k\right)+1+1=3.\left(3k^2+3k\right)+2\)
Thấy \(3.\left(3k^2+3k\right)+2\) chia 3 dư 2
\(\Rightarrow a^2+a\) chia 3 dư 2
\(\Rightarrow a\left(a+1\right)\) chia 3 dư 2
TH3: a chia 3 dư 2
\(\Rightarrow a^2=\left(3k+2\right)^2=\left(3k+2\right)\left(3k+2\right)=\left(3k+2\right).3k+\left(3k+2\right).2=9k^2+6k+6k+4\) \(=3.\left(3k^2+2k+2k\right)+4\)
\(\Rightarrow a^2+a=3.\left(3k^2+2k+2k\right)+4+3k+2=3.\left(3k^2+2k+2k+k\right)+6\)
\(=3.\left(3k^2+5k\right)+3.2=3.\left(3k^2+5k+2\right)\) chia hết cho 3
Như vậy tích 2 số tự nhiên liên tiếp luôn chia hết cho 3 hoặc chia 3 dư 2.
Mà \(\left(-3\right)^{20}+1=3^{20}+1\) chia 3 dư 1
Vậy \(\left(-3\right)^{20}+1\) không phải tích 2 số tự nhiên liên tiếp.
15 tháng 2 2016
Phân tích 19656 ra thừa số nguyên tố ta có:
19656=23.33.7.13=8.27.7.13
Từ đó biểu diễn 19656 dưới tích của 3 thừa số:
19656= (13.2).27.(7.4) ( 1 số bạn thắc mắc 2 và 4 lấy ở đâu ra thực chất nó từ 8=2.4)
=> 19656=27.26.28
Vậy 3 số tự nhiên đó bằng 26;27;28
LM
15 tháng 2 2016
phân tích 19656 ra thừa số nguyên tố
19656 = 2^3. 3^3. 7.13 = 8. 27 . 7.13
từ đó biểu diễn 19656 dưới dạng tích của 3 thừa số
19656 = (13.2) . 27. (7.4) = 26. 27. 28
vậy 3 số tự nhiên liên tiếp là 26, 27, 28
CM
3 tháng 9 2019
Chọn B.
Để tích các số chấm xuất hiện ở năm lần gieo là một số tự nhiên có tận cùng bằng 5 thì phải có ít nhất một lần ra mặt 5 chấm và các mặt khác ra mặt lẻ. Do đó xác suất cần tìm bằng
LM
10 tháng 3 2016
1. Xét số ab với a từ 0 đến 14 và b từ 0 đến 9. Vậy tổng của b (các chữ số hàng đơn vị) là 45*15=630. Tổng của các chữ số của a là 45+15. Với 45 là tổng các chữ số từ 0 đến 9, 15 là tổng các chữ số từ 10 đến 14. Và số 150 có tổng giá trị chữ số là 6. Vậy có tổng cộng 630+45+15+6=696
2.Tổng các chữ số: 4x2013=8052 và 8+5+0+2=15 số này chia hết cho 3 nên chia cho 15 sẽ dư là 1 số chia hết cho 3
Số này tận cùng là 4 nên chia cho 5 sẽ dư 4(không chia hết cho 3 vậy chia cho 15 dư 4+5=9 ( chia hết cho 3; nếu dư là 9+4=14 cũng không chia hết cho 3
Kết luận:Số dư là 9
3.không bít
4.Gọi a và b lần lượt là chữ số hàng chục và hàng đơn vị của số đó.Vậy số đó là 10a+b (a,b là số tự nhiên nhỏ hơn 10 và a#0).
(10a+b)/(a+b)=(10a+10b-9b)/(a+b)=
=10-9b/(a+b).
Hiệu này lớn nhất bằng 10 khi b=0 (a tùy ý)
Vậy bài này có 9 đáp án là 10,20,30,...,90.
2)a/b=a+b/10 (a,b là số tự nhiên nhỏ hơn 10 và b#0).
Vì b>=1 nên a/b<=a<a+b/10 =>pt trên vô nghiệm
Không có 2 chữ số a,b nào thỏa mãn ĐK bài toán.
LM
10 tháng 3 2016
1.Ta kết hợp 1 với 98 , 2 với 97 , 3 với 96 ......thành từng cặp có tổng bằng 99 thì mỗi tổng như vậy
có tổng các chữ số là 18 ( do 9 + 9 )
Có tất cả 49 tổng như vậy cộng thêm số 99 như vậy tổng các chữ số của số 1 2 3 4 5 6........98 99
là 18 * 50 = 900
Lại có : Ta kết hợp 100 với 149 , 101 với 148 , 102 với 147 ......thành từng cặp có tổng bằng 249
thì mỗi tổng như vậy có tổng các chữ số là 115 ( do 2+ 4 + 9 )
Có tất cả 25 tổng như vậy nên tổng các chữ số của số 100 101 102........147 148 149 là
15 * 25 = 375
Số 150 có tổng các chữ số là 6
Vậy có 900 + 375 + 6 = 1281
2.Ta gọi r là số dư của A khi chia A cho 15 => A = 15k + r (0 <= r <15).
Lại thấy A chia hết cho 3 (tổng các chữ số của A chia hết cho 3), theo tính chất chia hết của một tổng thì r phải chia hết cho 3 => r = 0, 3, 6, 9, 12. Dễ thấy A chia 5 dư 4 (vì A = 444...440 + 4) nên r chia 5 phải dư 4 (vì 15k đã chia hết cho 5), trong các số 0, 3, 6, 9, 12 thì chỉ có 9 chia 5 dư 4
VẬY số dư của A khi chia cho 15 là 9.
3.
4.gọi số đó là ab, a là hàng chục, b là hàng đơn vị; thế thì a, b là số tự nhiên 1≤a≤9 và 0≤b≤9,
ab/(a+b) là lớn nhất khi a+b nhỏ nhất khi a=1, b=0 vậy số đó là 10
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
30 tháng 7 2023
Trung bình cộng của ba số tự nhiên liên tiếp bằng số thứ hai và bằng:
2256 : 3 = 752
Số thứ nhất là: 752 - 1 = 751
Đáp số: 751
AH
Akai Haruma
Giáo viên
9 tháng 4 2023
Lời giải:
Gọi ba số tự nhiên liên tiếp là $a,a+1, a+2$. Tổng của chúng là:
$a+(a+1)+(a+2)=1194$
$a+a+a+1+2=1194$
$a\times 3+3=1194$
$a\times 3=1194-3=1191$
$a=1191:3=397$
Số lớn nhất trong 3 số: $397+2=399$
TP
30 tháng 8
- Gọi số đầu tiên trong dãy các số tự nhiên liên tiếp là: x
Ta có:
x + (x + 1) + (x + 2) = 1194
x . 3 + (1 + 2) = 1194
x . 3 + 3 = 1194
x . 3 = 1194 - 3
x . 3 = 1191
x = 1191 : 3
x = 397
=> Số lớn nhất trong dãy ba số tự nhiên liên tiếp là: (x + 2)
=> Số đó là: 397 + 2 = 399
Vậy số đó là 399
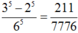
Ta có tích 4 số tự nhiên liên tiếp cần tìm là 93024
Vì 93024 ko có chữ số tận cùng là 0 hoặc 5
Suy ra ko có số nào trong đó chứa chữ số tận cùng là 0 hoặc 5
Ta có: 10.10.10.10=10000 (10000<93024)
Suy ra mỗi số tự nhiên liên tiếp trong đó lớn hơn 10 mà 20.20.20.20=160000 (160000>93024)
Suy ra các số tự nhiên liên tiếp nhỏ hơn 20
Mà trong 4 số tự nhiên liên tiếp không có số nào có chữ số tận cùng bằng 0 hoặc 5
Suy ra:
1.Các số tự nhiên liên tiếp đó là:11,12,13,14
11.12.13.14=1716 (loại vì 1716<93024)
2.Các số tự nhiên liên tiếp là:16,17,18,19
16.17.18.19=93024 (chọn )
ok! question