NT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VD
1
25 tháng 1 2022
a: =>1+2+...+x=120
=>x(x+1)/2=120
=>x(x+1)=240
=>\(x^2+x-240=0\)
\(\Delta=1^2-4\cdot1\cdot\left(-240\right)=961>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-1-31}{2}=\dfrac{-32}{2}=-16\left(loại\right)\\x_2=\dfrac{-1+31}{2}=15\left(nhận\right)\end{matrix}\right.\)
CM
14 tháng 1 2017
Chọn đáp án B
Phương pháp
+) Tính số phần tử của không gian mẫu.
+) Gọi A là biến cố: “Trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp”
=> A “Trong 3 số tự nhiên được chọn có 2 số tự nhiên liên tiếp”.
+) Tính số phần tử của biến cố A .
+) Tính xác suất của biến cố A , từ đó tính xác suất biến cố A.
Cách giải
Chọn ngẫu nhiên 3 số tự nhiên ⇒ n Ω = C 2019 3
Gọi A là biến cố: “Trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp”
=> A : “Trong 3 số tự nhiên được chọn có 2 số tự nhiên liên tiếp”.
Số cách chọn 3 trong 2019 số, trong đó có 2 số tự nhiên liên tiếp, có 2018.2017 cách (có bao gồm các bộ 3 số tự nhiên liên tiếp).
Số cách cả 3 số tự nhiên liên tiếp, có 2017 cách.
CM
19 tháng 6 2017
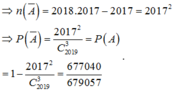
Đáp án D
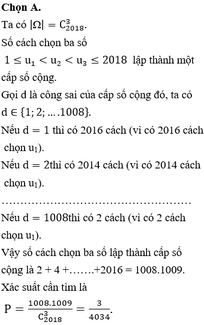
Gọi bộ 5 số cần chọn là 1 ≤ a 1 < a 2 < a 3 < a 4 < a 5 ≤ 20.
Để không có hai số nào liên tiếp thì
1 ≤ a 1 < a 2 − 1 < a 3 − 2 < a 4 − 3 < a 5 − 4 ≤ 16.
Đặt b 1 = a 1 ; b 2 = a 2 − 1 ; b 3 = a 3 − 2 ; b 4 = a 4 − 3 ; b 5 = a 5 − 4.
Với b 1 < b 2 < b 3 < b 4 < b 5 suy ra không có bộ 5 số nào chứa hai số tự nhiên liên tiếp.
Khi đó 1 ≤ b 1 < b 2 < b 3 < b 4 < b 5 ≤ 16.
Chọn bộ 5 số b 1 ; b 2 ; b 3 ; b 4 ; b 5 từ 16 số là tổ hợp chập 5 của 16.
Vậy có tất cả C 16 5 bộ thỏa mãn yêu cầu bài toán
CM
17 tháng 6 2017
Đáp án D
Nếu A = 1 ; 2 ; ....9 thì chỉ có duy nhất 1 cách là 1 ; 3 ; 5 ; 7 ; 9 khi đó số cách bằng C 5 5 = C 9 − 4 5
Nếu A = 1 ; 2 ; 3...10 thì có
1 ; 3 ; 5 ; 7 ; 9 ; 1 ; 4 ; 6 ; 8 ; 10 ; 1 ; 3 ; 6 ; 8 ; 10 ; 1 ; 3 ; 5 ; 8 ; 10 ; 1 ; 3 ; 5 ; 7 ; 10 ; 2 ; 4 ; 6 ; 8 ; 10 có 6 cách bằng 6 = C 6 5 . Như vậy đáp án sẽ là C 16 5
TT
5
15 tháng 2 2016
Phân tích 19656 ra thừa số nguyên tố ta có:
19656=23.33.7.13=8.27.7.13
Từ đó biểu diễn 19656 dưới tích của 3 thừa số:
19656= (13.2).27.(7.4) ( 1 số bạn thắc mắc 2 và 4 lấy ở đâu ra thực chất nó từ 8=2.4)
=> 19656=27.26.28
Vậy 3 số tự nhiên đó bằng 26;27;28
LM
15 tháng 2 2016
phân tích 19656 ra thừa số nguyên tố
19656 = 2^3. 3^3. 7.13 = 8. 27 . 7.13
từ đó biểu diễn 19656 dưới dạng tích của 3 thừa số
19656 = (13.2) . 27. (7.4) = 26. 27. 28
vậy 3 số tự nhiên liên tiếp là 26, 27, 28
NT
4
14 tháng 2 2016
Ta có tích 4 số tự nhiên liên tiếp cần tìm là 93024
Vì 93024 ko có chữ số tận cùng là 0 hoặc 5
Suy ra ko có số nào trong đó chứa chữ số tận cùng là 0 hoặc 5
Ta có: 10.10.10.10=10000 (10000<93024)
Suy ra mỗi số tự nhiên liên tiếp trong đó lớn hơn 10 mà 20.20.20.20=160000 (160000>93024)
Suy ra các số tự nhiên liên tiếp nhỏ hơn 20
Mà trong 4 số tự nhiên liên tiếp không có số nào có chữ số tận cùng bằng 0 hoặc 5
Suy ra:
1.Các số tự nhiên liên tiếp đó là:11,12,13,14
11.12.13.14=1716 (loại vì 1716<93024)
2.Các số tự nhiên liên tiếp là:16,17,18,19
16.17.18.19=93024 (chọn )
29 tháng 2 2016
(Từ 1 đến 999) có 300 chữ số 1.
Vì hàng đơn vị có 100 chữ hàng chục có 100 chữ số
hàng trăm có 100 chữ số 1.
từ 1000 đến 1999 có 1300 chữ số 1
.vì hàng nghìn có 1000 chữ số 1, 3 hàng :trăm, chục, đơn vị có 300 chữ số 1
.Từ 2000 đến 2014 có 7 chữ số 1. Vậy tổng cộng có 1607 chữ số 1
Trả lời: Trong dãy đó có tất cả 1607 chữ số 1.
lớp mấy
Đặt tích 2 số tự nhiên liên tiếp là \(a\left(a+1\right)=a^2+a\)
Ta sẽ xét xem tích 2 số tự nhiên liên tiếp chia cho 3 dư bao nhiêu.
TH1: a chia hết cho 3
\(\Rightarrow\)a2 chia hết cho 3 và a cũng chia hết cho 3
\(\Rightarrow a^2+a\) chia hết cho 3
\(\Rightarrow a\left(a+1\right)\) chia hết cho 3
TH2: a chia 3 dư 1 -> a có dạng 3k+1
\(\Rightarrow a^2=\left(3k+1\right)^2=\left(3k+1\right)\left(3k+1\right)=\left(3k+1\right)3k+\left(3k+1\right).1=9k^2+3k+3k+1\)\(=3.\left(3k^2+k+k\right)+1\)
\(\Rightarrow a^2+a=3.\left(3k^2+k+k\right)+1+3k+1=3.\left(3k^2+k+k+k\right)+1+1=3.\left(3k^2+3k\right)+2\)
Thấy \(3.\left(3k^2+3k\right)+2\) chia 3 dư 2
\(\Rightarrow a^2+a\) chia 3 dư 2
\(\Rightarrow a\left(a+1\right)\) chia 3 dư 2
TH3: a chia 3 dư 2
\(\Rightarrow a^2=\left(3k+2\right)^2=\left(3k+2\right)\left(3k+2\right)=\left(3k+2\right).3k+\left(3k+2\right).2=9k^2+6k+6k+4\) \(=3.\left(3k^2+2k+2k\right)+4\)
\(\Rightarrow a^2+a=3.\left(3k^2+2k+2k\right)+4+3k+2=3.\left(3k^2+2k+2k+k\right)+6\)
\(=3.\left(3k^2+5k\right)+3.2=3.\left(3k^2+5k+2\right)\) chia hết cho 3
Như vậy tích 2 số tự nhiên liên tiếp luôn chia hết cho 3 hoặc chia 3 dư 2.
Mà \(\left(-3\right)^{20}+1=3^{20}+1\) chia 3 dư 1
Vậy \(\left(-3\right)^{20}+1\) không phải tích 2 số tự nhiên liên tiếp.