Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có hai trường hợp như sau :
TH1
\(x-2016\ge0\Leftrightarrow x\ge2016\) thì \(A=x-2016+x-1=2x-2017\ge2.2016-2017=2015\)
TH2
\(x-2016\le0\Leftrightarrow x\le2016\) thì \(A=2016-x+x-1=2015\)
vì vậy GTNN của A=2015
dấu bằng xảy ra khi \(x\le2016\)

\(\left|2x-1\right|=\dfrac{3}{2}\\ \Rightarrow\left[{}\begin{matrix}2x-1=\dfrac{3}{2}\\2x-1=-\dfrac{3}{2}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=-\dfrac{1}{4}\end{matrix}\right.\)
Thay \(x=\dfrac{5}{4}\) vào D ta có:
\(D=4x+3=4.\dfrac{5}{4}+3=5+3=8\)
Thay \(x=-\dfrac{1}{4}\) vào D ta có:
\(D=4.\dfrac{-1}{4}+3=-1+3=2\)
Để \(D=\dfrac{3}{2}\)
\(\Leftrightarrow4x+3=\dfrac{3}{2}\\ \Leftrightarrow4x=-\dfrac{3}{2}\\ \Leftrightarrow x=-\dfrac{3}{8}\)

a: \(P\left(x\right)=3x^2-x-1\)
\(Q\left(x\right)=-3x^2-4x-2\)
b: \(G\left(x\right)=3x^2-x-1+3x^2+4x+2=6x^2+3x+1\)
c: Để G(x)-6x-1=0 thì 6x2-3x=0
=>3x(2x-1)=0
=>x=0 hoặc x=1/2

`a)`
`A(x) + B(x) = 2x - 4x^2 + 1 + x^3 - 4x^2 + 5 - 2x`
`= x^3 - ( 4x^2 + 4x^2 ) + ( 2x - 2x ) + ( 1+ 5 )`
`= x^3 - 8x^2 + 6`
__________________________________________________________
`b)`
`P(x) + B(x) = A(x)`
`=>P(x) = A(x) - B(x)`
`=>P(x) = 2x - 4x^2 + 1 + x^3 + 4x^2 - 5 + 2x`
`=>P(x) = x^3 + ( -4x^2 + 4x^2 ) + ( 2x + 2x ) + ( 1 - 5 )`
`=>P(x) = x^3 + 4x - 4`

26:
A=12x^2+10x-6x-5-(12x^2-8x+3x-2)
=12x^2+4x-5-12x^2+5x+2
=9x-3
Khi x=-2 thì A=-18-3=-21
25:
b: \(\left(y-3\right)\left(y^2+y+1\right)-y\left(y^2-2\right)\)
=y^3+y^2+y-3y^2-3y-3-y^3+2y
=-2y^2-3

\(E=\dfrac{\dfrac{5}{2}\left(2x^2+3\right)+\dfrac{15}{2}}{2x^2+3}=\dfrac{5}{2}+\dfrac{15}{2\left(2x^2+3\right)}\)
Do \(2x^2+3\ge3;\forall x\Rightarrow\dfrac{15}{2\left(2x^2+3\right)}\le\dfrac{15}{2.3}=\dfrac{5}{2}\)
\(\Rightarrow E\le\dfrac{5}{2}+\dfrac{5}{2}=5\)
\(E_{max}=5\) khi \(x=0\)

biểu thức 2x^3 bằng biểu thức nào sau đây
A: 2x^3 B: 8x^3 C: 6x^3 D:8x
HT
@@@@@@
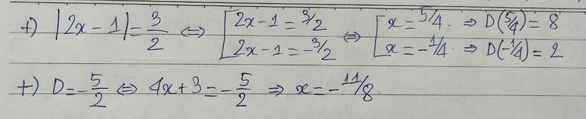
=(2x-1)(4x^2+2x+1):(2x-1)
=4x^2+2x+1
bn lm lại rõ ràng đc ạ