Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

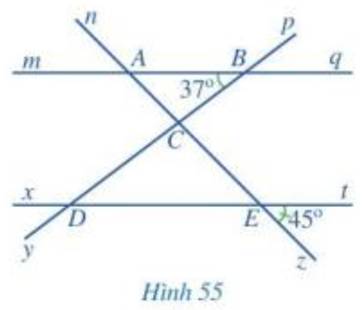
a) Các cặp góc đồng vị bằng nhau là: góc mAn và xEn; góc mAz và xEz; góc nAq và nEt; góc qAz và tEz; góc pBq và pDt; góc qBy và tDy; góc mBy và xDy; góc pBm và pDx
b) Vì mq // xt nên \(\widehat {BAC} = \widehat {zEt}\) ( 2 góc đồng vị) nên \(\widehat {BAC} = 45^\circ \).
Vì mq // xt nên \(\widehat {CDE} = \widehat {ABC}\) ( 2 góc so le trong) nên \(\widehat {CDE} = 37^\circ \).
c)
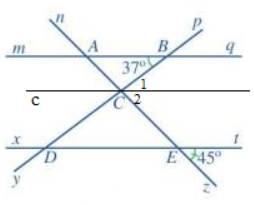
Bạn Nam nói đúng vì:
Vì c // mq nên \(\widehat {ABC} = \widehat {{C_1}}\) ( 2 góc so le trong) nên \(\widehat {{C_1}} = 37^\circ \)
Vì c // xt nên \(\widehat {CED} = \widehat {{C_2}}\) ( 2 góc so le trong) nên \(\widehat {{C_2}} = 45^\circ \)
Vì \(\widehat {{C_1}} + \widehat {{C_2}} = \widehat {BCE}\) nên \(\widehat {BCE} = \widehat {{C_1}} + \widehat {{C_2}} = 37^\circ + 45^\circ = 82^\circ \)

\(a,\)So le trong: \(E_1 và F_2;E_2 và F_1\)
Đồng vị: \(E_1 và F_4;E_2 và F_3;E_3 và F_2;E_4 và F_1\)
Trong cùng phía: \(E_1 và F_1;E_2 và F_2\)
\(b,\widehat{F_1}=\widehat{F_3}=120^0\left(đối.đỉnh\right)\\ \widehat{F_2}+\widehat{F_3}=180^0\left(kề.bù\right)\Rightarrow\widehat{F_2}=180^0-120^0=60^0\\ \widehat{F_2}=\widehat{F_4}-60^0\left(đối.đỉnh\right)\)
\(c,C_1:\widehat{F_2}=\widehat{E_3}\left(=60^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(a//b\)
\(C_2:\)\(\widehat{E_1}=\widehat{E_3}=60^0\left(đối.đỉnh\right)\Rightarrow\widehat{E_1}=\widehat{F_2}\left(=60^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(a//b\)
a. Các cặp góc:
- So le trong là: \(\widehat{E_1}\) và \(\widehat{F_2};\widehat{E_2}\) và \(\widehat{F_1}\)
- Đồng vị là: \(\widehat{E_4},\widehat{F_1};\widehat{E_3},\widehat{F_2};\widehat{E_2},\widehat{F_3};\widehat{E_1},\widehat{F_4}\)
- Trong cùng phía là: \(\widehat{E_1},\widehat{F_1};\widehat{E_2},\widehat{F_2}\)
b. Ta có: \(\widehat{F_1}=\widehat{F_3}=120^o\) (đối đỉnh)
\(\widehat{F_2}=180^o-\widehat{F_1}=180^o-120^o=60^o\)
\(\widehat{F_3}=120^o\)
\(\widehat{F_4}=\widehat{F_2}=60^o\) (đối đỉnh)
c.
C1: Ta có: \(\widehat{E_1}=\widehat{E_3}=60^o\) (đối đỉnh)
Ta thấy: \(\widehat{E_1}=\widehat{F_2}=60^o\)
=> a//b (so le trong)
C2: Ta có: \(\widehat{E_2}=180^o-\widehat{E_3}=180^o-60^o=120^o\)
Ta thấy: \(\widehat{E_2}=\widehat{F_1}=120^o\)
=> a//b (so le trong)

a)
b) \(\widehat{A_3}=\widehat{B_3}=130^o\) ( đồng vị; a//b)
c) \(\widehat{A_3}=\widehat{B_1}=130^o\) ( so le trong; a//b)
d)Cặp góc trong cùng phía là: \(\widehat{A_3}\) và \(\widehat{B_2}\)
Vì \(\widehat{A_3}\) và \(\widehat{B_2}\) là hai góc trong cùng phía:
nên: \(\widehat{A_3}+\widehat{B_2}=130^o+50^o=180^o\)
Vậy \(\widehat{A_3}+\widehat{B_3}=180^o\)
![]() ^...^
^...^ ![]() ^_^ ( Bài mk làm có gì ko hiểu bạn cứ hỏi mk nhé)
^_^ ( Bài mk làm có gì ko hiểu bạn cứ hỏi mk nhé)

A 1 và B2 bằng nhau vì: theo định lý ( một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau )
A 1 và B1 bằng nhau vì theo định lý ( một đường thẳng cát hai đường thẳng song song thì hai góc so le trong bằng nhau )
Nói tóm gọm lại là bn chỉ trả lời hai góc này bằng nhau vì : theo đinh lý là xong
Mik học r
cảm ơn cô ạ
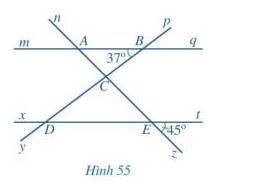
a, Các góc đồng vị bằng nhau là:
\(\widehat{nAm}\) = \(\widehat{AEx}\); \(\widehat{mAE}\) = \(\widehat{zED}\); \(\widehat{nAB}\) = \(\widehat{AEt}\)
\(\widehat{qAE}\) = \(\widehat{tEz}\); \(\widehat{pBq}\) = \(\widehat{BDE}\); \(\widehat{qBC}\) = \(\widehat{EDy}\); \(\widehat{pBA}\) = \(\widehat{BDx}\); \(\widehat{ABD}\)=\(\widehat{xDy}\)
b, Các góc so le trong:
\(\widehat{ABC}\) = \(\widehat{CDE}\); \(\widehat{mAC}\) = \(\widehat{CEt}\); \(\widehat{BAC}\) = \(\widehat{CED}\); \(\widehat{qBc}\) = \(\widehat{CDx}\)
c, \(\widehat{BAC}\) = \(\widehat{zEt}\) = 450
\(\widehat{CDE}\) = \(\widehat{ABC}\) = 390
d, \(\widehat{BCE}\) = \(\widehat{CDE}\) + \(\widehat{CED}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó.
\(\widehat{CED}\) = \(\widehat{zEt}\) = 450 (hai góc đối đỉnh)
\(\widehat{BCE}\) = 390 + 450 = 840