

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a) Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔAHB∼ΔCAB(g-g)

a) Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{ACH}\) chung
Do đó: ΔABC\(\sim\)ΔHAC(g-g)
b) Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow HC^2=AC^2-AH^2=30^2-24^2=324\)
hay HC=18(cm)
Ta có: ΔABC∼ΔHAC(cmt)
nên \(\dfrac{AB}{HA}=\dfrac{BC}{AC}=\dfrac{AC}{HC}\)(Các cặp cạnh tương ứng tỉ lệ)
\(\Leftrightarrow\dfrac{AB}{24}=\dfrac{BC}{30}=\dfrac{30}{18}=\dfrac{5}{3}\)
Suy ra: \(\left\{{}\begin{matrix}\dfrac{AB}{24}=\dfrac{5}{3}\\\dfrac{BC}{30}=\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=40\left(cm\right)\\BC=50\left(cm\right)\end{matrix}\right.\)
Vậy: HC=18cm; AB=40cm; BC=50cm

a. Ta thấy \(S\Delta ABC=\frac{1}{2}AB.AB=\frac{1}{2}BC.AH\Rightarrow AH=24\)
Vậy \(BH=\sqrt{AB^2-AH^2}=18\)
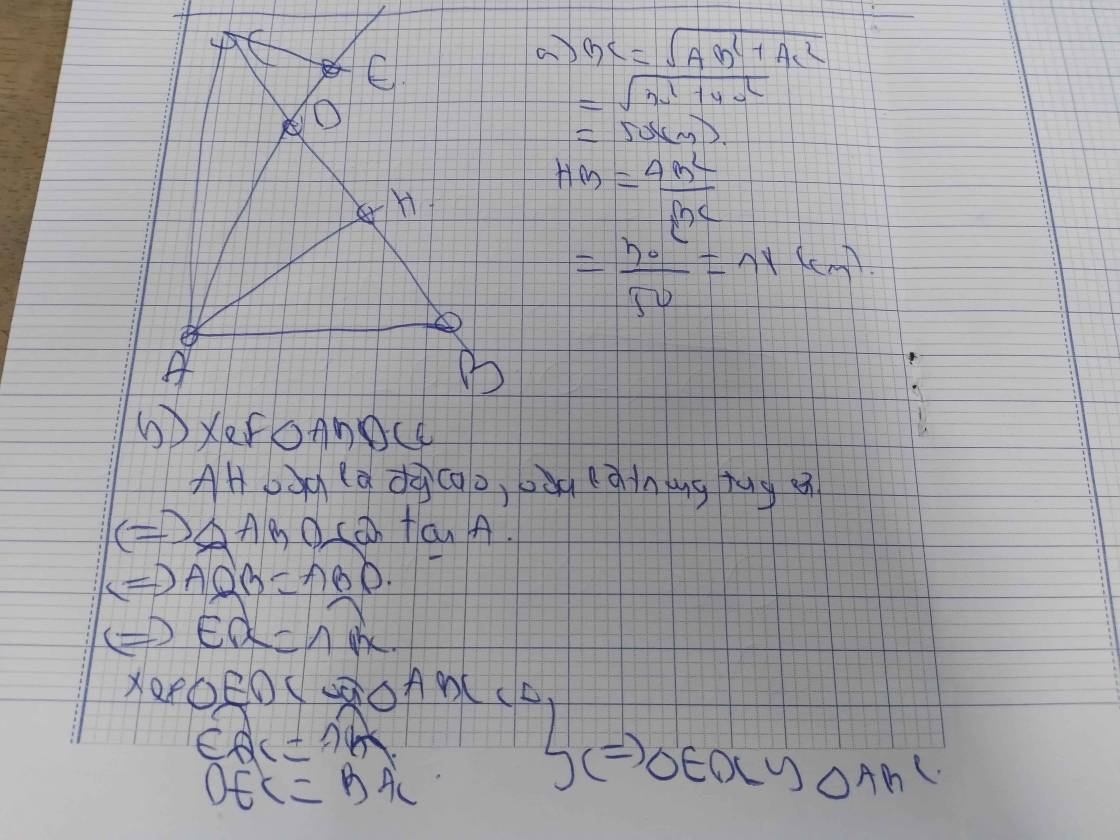
b. Xét tam giác ABC và EDC có:
góc A = góc E vuông
góc ABC= góc EDC (cùng bằng góc BDA)
Vậy \(\Delta ABC\sim\Delta EDC\left(g-g\right)\)
Vậy \(\frac{AB}{ED}=\frac{AC}{EC}\Rightarrow AB.EC=ED.AC\)
c. Ta thấy \(\frac{S\Delta EDC}{S\Delta ABC}=\left(\frac{DC}{BC}\right)^2=\left(\frac{50-18.2}{50}\right)^2=\frac{49}{625}\)
ta tính đc diện tích ABC từ đó suy ra diện tích EDC.