
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

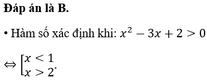

Chọn C.
Phương pháp : Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải :
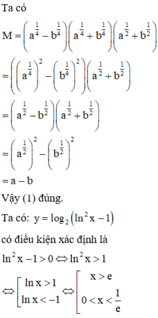
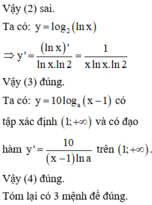


Hình ảnh trên là một phần đồ thị của y trên tập xác định. Ta thấy rằng hàm số đạt cực đại tại x = 2 nhưng không chắc rằng có còn điểm cực đại nào khác trên những khoảng rộng hơn hay không (I) sai, (III) đúng.
Hàm số không xác định tại x = 1 nên không thể đạt cực tiểu tại điểm này =>(II) sai.
Chọn B

Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .

Chọn A.
(I) sai f xđ trên R
(II) sai hs có 2 điểm cực trị
(III) ,(IV) đúng

Đáp án A
Áp dụng lý thuyết “lũy thừa với số mũ nguyên âm thì cơ số phải khác 0”
Do đó hàm số y = x − 1 − 2 + log 3 x + 1 xác định khi
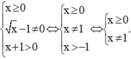
Lỗi sai:
* Các em không nhớ tập xác định của hàm lũy thừa với các trường hợp số mũ khác nhau, ở đây mũ nguyên âm thì cơ số phải khác 0.
* Chú ý (SGK giải tích 12 trang 57). Tập xác định của hàm số lũy thừa y = x α tùy thuộc vào giá trị của α . Cụ thể:
- Với α nguyên dương, tập xác định là R.
- Với α nguyên âm hoặc bằng 0, tập xác định là R\{0}
- Với α không nguyên, tập xác định là 0 ; + ∞