Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Đặt $\sqrt{x+2}=t(t\geq 0)$ thì pt trở thành:
$t^2-2-2t-m-3=0$
$\Leftrightarrow t^2-2t-(m+5)=0(*)$
Để PT ban đầu có 2 nghiệm pb thì PT $(*)$ có 2 nghiệm không âm phân biệt.
Điều này xảy ra khi \(\left\{\begin{matrix} \Delta'=1+m+5>0\\ S=2>0\\ P=-(m+5)\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m>-6\\ m\leq -5\end{matrix}\right.\)
Đáp án B.

Ta có: 2 x + 1 > 3 x - 2 - x - 3 < 0 ⇔ - x > - 3 - x < 3 ⇔ x < 3 x > - 3 ⇔ - 3 < x < 3

Điều kiện: x > 2.
Với điều kiện trên , phương trình đã cho trở thành:
x - 3 = x - 3 ⇔ x - 3 ≥ 0 ⇔ x ≥ 3
Kết hợp điều kiện, tập nghiệm của phương trình là S = [ 3 ; + ∞ )

Ta có :
1 x - 1 ≥ 1 x + 2 - 1 ⇔ 1 x - 1 - 1 x + 2 + 1 ≥ 0 ⇔ x + 2 - x - 1 + x - 1 . x + 2 x - 1 . x + 2 ≥ 0 ⇔ 3 + x 2 + 2 x - x - 2 x - 1 . x + 2 ≥ 0 ⇔ x 2 + x + 1 x - 1 . x + 2 ≥ 0 ( * )
Lại có: x 2 + x + 1 = x 2 + 2 . x . 1 2 + 1 4 + 3 4 = x + 1 2 2 + 3 4 > 0 ∀ x
Do đó, (*) ⇔ x - 1 . x + 2 > 0 ⇔ [ x > 1 x < - 2
Tập nghiệm của bất phương trình: S = - ∞ ; - 2 ∪ 1 ; + ∞
Chọn A.

Ta có: m - 1 x + 6 ≥ 0 ; x + 2 ≥ 0 . Do đó,
m - 1 x + 6 + x + 2 = 0 ⇔ m - 1 x + 6 = 0 x + 2 = 0 ⇔ m - 1 . - 2 + 6 = 0 x = - 2 ⇔ - 2 m + 2 + 6 = 0 x = - 2 ⇔ m = 4 x = - 2
Chọn A.

x 2 - x > x + 1 ⇔ [ x + 1 < 0 x 2 - x ≥ 0 x + 1 ≥ 0 x 2 - x > 0 ⇔ [ x < - 1 [ x ≥ 1 x ≤ 0 x ≥ - 1 x 2 - x > x 2 + 2 x + 1
[ x < - 1 x ≥ - 1 - 3 x > 1 ⇔ [ x < - 1 x ≥ - 1 x < - 1 3 ⇔ [ x < - 1 - 1 ≤ x ≤ - 1 3 ⇔ x < - 1 3
Chọn B.
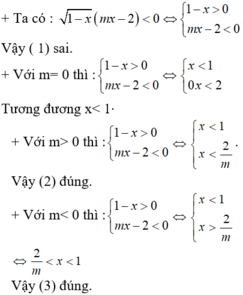
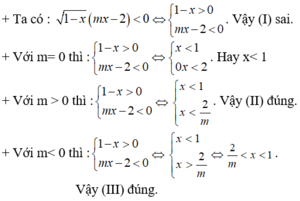
2 x + 1 = x - 1 ⇔ 2 x + 1 ≥ 0 x - 1 ≥ 0 2 x + 1 = x 2 - 2 x + 1 ⇔ x ≥ - 1 2 x ≥ 1 - x 2 + 4 x = 0 ⇔ x ≥ 1 [ x = 0 ⇔ x = 4 x = 4
Chọn A.