Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(AC=\sqrt{20^2-12^2}=16\left(cm\right)\)
Xét ΔACB có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=20/7
=>DB=60/7cm; DC=80/7cm

Hình bạn tự vẽ nha
| GT | ΔACB vuông tại A, BD là phân giác, AB/CB=3/5; AC=16cm |
| KL | a: AB=?; BC=? b: AD=?; CD=? |
a: AB/BC=3/5
=>AB/3=BC/5=k
=>AB=3k; BC=5k
BC^2=AB^2+AC^2
=>16k^2=16^2=256
=>k^2=16
=>k=4
=>AB=12cm; CB=20cm
b: BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=16/8=2
=>AD=6cm; CD=10cm

Với `(AB)/(BC) = 3/5`
`=> (AB)/3 = (BC)/5`
Đặt `(AB)/3 = (BC)/5 = k (k > 0)`
`=> AB = 3k; BC = 5k`
Áp dụng định lý pitago vào tam giác `ABC` vuông tại `A`
`=> AB^2 + AC^2 = BC^2`
`=> (3k)^2 + 16^2 = (5k)^2`
`=> 9k^2 + 256 = 25k^2`
`=> 16k^2 = 256`
`=> k^2 = 16`
`=> k^2 = 4^2`
`=> k = 4 (`Vì `k > 0)`
Khi đó: `AB = 3k = 4 . 3 = 12 (cm)`
`BC = 5k = 5 . 4 = 20 (cm)`
b) Tam giác `ABC` có BD là tia phân giác của tam giác `ABC`. Áp dụng tính chất đường phân giác trong tam giác
`=> (AD)/(AB) = (DC)/(BC) `
`=> (AD)/12 = (DC)/20`
Áp dụng tính chất dãy tỉ số bằng nhau
`=> (AD)/12 = (DC)/20 = (AD + DC)/(12 + 20) = 16/32 = 1/2`
`=> AD = 1/2 xx 12 = 6 (cm) ; DC = 1/2 xx 20 = 10 (cm)`
a: AB/BC=3/5
=>AB/3=BC/5=k
=>AB=3k; BC=5k
BC^2=AB^2+AC^2
=>16k^2=16^2=256
=>k^2=16
=>k=4
=>AB=12cm; CB=20cm
b: BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=16/8=2
=>AD=6cm; CD=10cm

a: AB/BC=3/5
=>AB/3=BC/5=k
=>AB=3k; BC=5k
BC^2=AB^2+AC^2
=>16k^2=16^2=256
=>k^2=16
=>k=4
=>AB=12cm; CB=20cm
b: BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=16/8=2
=>AD=6cm; CD=10cm

3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)

Xét ΔBAC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{12}=\dfrac{CD}{20}\)
mà BD+CD=28cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{12}=\dfrac{CD}{20}=\dfrac{BD+CD}{12+20}=\dfrac{28}{32}=\dfrac{7}{8}\)
Do đó: BD=10,5cm; CD=17,5cm
Xét ΔBAC có
DE//AB
nên \(\dfrac{DE}{AB}=\dfrac{CD}{BC}\)
\(\Leftrightarrow DE=\dfrac{17.5}{28}\cdot12=7.5\left(cm\right)\)

* Trong △ ABC, ta có:
AD là đường phân giác của ∠ (BAC)
Suy ra: 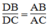 (tính chất tia phân giác)
(tính chất tia phân giác)
Suy ra: 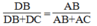
Suy ra: 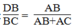
Suy ra: 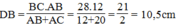
Vậy DC = BC - DB = 28 - 10,5 = 17,5 (cm)
* Trong △ ABC, ta có: DE // AB
Suy ra: 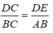 (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)
Vậy: 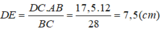

Xét \(\Delta ABC\) vuông tại A có \(AB^2+AC^2=BC^2\) (định lý Pytago)
\(\Rightarrow BC^2=12^2+16^2=20^2\Rightarrow BC=20\).
Theo tính chất đường phân giác trong tam giác ABC ta có:
\(\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{CD+BD}{AC+AB}=\dfrac{BC}{AC+AB}=\dfrac{20}{12+16}=\dfrac{5}{7}\Rightarrow BD=\dfrac{60}{7};CD=\dfrac{80}{7}\).
Ta có \(AH.BC=AB.AC\left(=2S_{ABC}\right)\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{48}{5}\).
Từ đó \(BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-\left(\dfrac{48}{5}\right)^2}=\dfrac{36}{5}\).
Suy ra \(HD=\left|BD-BH\right|=\left|\dfrac{48}{5}-\dfrac{36}{5}\right|=\dfrac{12}{5}\).
\(AD=\sqrt{AH^2+HD^2}=\dfrac{12\sqrt{17}}{5}\).

Để so sánh AD và DE, chúng ta cần tìm hiểu về các đặc điểm của tam giác ABC và các điểm B, D, E.
Với tam giác ABC, góc A bằng 90 độ và tia phân giác BD của góc B (D thuộc AC). Trên cạnh BC, ta lấy điểm E sao cho BE bằng BA.
Để so sánh AD và DE, chúng ta cần biết thêm về vị trí của các điểm A, B, C, D, E trên đường thẳng AC và BC.
Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>DA=DE
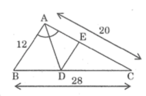
Xét ΔACB có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=20/7
=>DB=60/7cm; DC=80/7cm