K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 9 2021
1) \(=\sqrt{\left(\sqrt{3}-1\right)^2}=\sqrt{3}-1\)
2) \(=\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}=\sqrt{3}+\sqrt{2}\)
3) \(=\sqrt{\left(\sqrt{5}-\sqrt{2}\right)^2}=\sqrt{5}-\sqrt{2}\)
5) \(=\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}=\sqrt{5}+\sqrt{3}\)
6) \(=\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}=\sqrt{7}-\sqrt{3}\)
7) \(=\sqrt{\left(3+\sqrt{2}\right)^2}=3+\sqrt{2}\)
24 tháng 7 2019
b)\(\sqrt{17-12\sqrt{2}}\)
=\(\sqrt{9-2.3.2\sqrt{2}+8}\)
=\(\sqrt{\left(3-2\sqrt{2}\right)^2}\)
= \(3-2\sqrt{2}\)
21 tháng 9 2021
Câu 1. Biến đổi biểu thức trong căn thành một bình phương một tổng hay một hiệu rồi từ đó phá bớt một lớp căn
a/\(\sqrt{41+12\sqrt{5}}\)
25 tháng 6 2021
`(sqrtx+2)/(sqrtx-3)-(sqrtx+1)/(sqrtx-2)-(3(sqrtx-1))/(x-5sqrtx+6)`
đk:`x>=0,x ne 4,x ne 9`
`=((sqrtx+2)^2-(sqrtx+1)(sqrtx+3)-3(sqrtx-1))/(x-5sqrtx+6)`
`=(x+4sqrtx+4-x-4sqrtx-3-3sqrtx+3)/(x-5sqrtx+6)`
`=(4-3sqrtx)/(x-5sqrtx+6)`
6 tháng 6 2021
Bài 2:
a)\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}}=-4\) (đk: \(x\ge2\))
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9\left(x-2\right)}+\dfrac{6}{\sqrt{81}}\sqrt{x-2}=-4\)
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-2\sqrt{x-2}+\dfrac{2}{3}\sqrt{x-2}=-4\)
\(\Leftrightarrow-\sqrt{x-2}=-4\) \(\Leftrightarrow x-2=16\)
\(\Leftrightarrow x=18\) (thỏa)
Vậy...
b)\(\sqrt{9x^2+12x+4}=4x\)(Đk:\(9x^2+12x+4\ge0\))
\(\Leftrightarrow\left\{{}\begin{matrix}4x\ge0\\9x^2+12x+4=16x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+12x+4=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+14x-2x+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(x-2\right)\left(-7x-2\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x=2\\x=-\dfrac{2}{7}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x=2\) (tm đk)
Vậy...
c) \(\sqrt{x-2\sqrt{x-1}}=\sqrt{x-1}\) (đk: \(x\ge1\))
\(\Leftrightarrow x-2\sqrt{x-1}=x-1\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{1}{2}\) \(\Leftrightarrow x=\dfrac{5}{4}\) (tm)
Vậy...
25 tháng 8 2020
a)
= \(\sqrt{18-6\sqrt{6}+3}\)
= \(\sqrt{\left(3\sqrt{2}\right)^2-2\cdot3\sqrt{2}\cdot\sqrt{3}+\left(\sqrt{3}\right)^2}\)
= \(\sqrt{\left(3\sqrt{2}-\sqrt{3}\right)^2}\)
= \(|3\sqrt{2}-\sqrt{3}|\)
= \(3\sqrt{2}-\sqrt{3}\)
b)
= \(\sqrt{\frac{7}{2}-\sqrt{7}+\frac{1}{2}}\)
= \(\sqrt{\left(\sqrt{\frac{7}{2}}\right)^2+2\cdot\sqrt{\frac{7}{2}}\cdot\sqrt{\frac{1}{2}}+\left(\sqrt{\frac{1}{2}}\right)^2}\)
= \(\sqrt{\left(\sqrt{\frac{7}{2}}+\sqrt{\frac{1}{2}}\right)^2}\)
= \(|\sqrt{\frac{7}{2}}+\sqrt{\frac{1}{2}}|\)
= \(\sqrt{\frac{7}{2}}+\sqrt{\frac{1}{2}}\)
c)
= \(\sqrt{3+2\sqrt{3}+1}\)
= \(\sqrt{\left(\sqrt{3}\right)^2+2\cdot\sqrt{3}\cdot1+1^2}\)
= \(\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\)
d)
Đặt t = \(\sqrt{x-1}\left(ĐK:t\ge0\right)\)
= \(\sqrt{t^2+1-2t}\)
= \(\sqrt{\left(t+1\right)^2}\)
\(=t+1\)
= \(\sqrt{x-1}+1\)
25 tháng 8 2020
\(\sqrt{21-6\sqrt{6}}=\sqrt{18-2\sqrt{9}\sqrt{6}+3}=\sqrt{\left(\sqrt{18}\right)^2-2\sqrt{18}\sqrt{3}+\left(\sqrt{3}\right)^2}\)
\(=\sqrt{\left(\sqrt{18}+\sqrt{3}\right)^2}=\sqrt{18}+\sqrt{3}=\sqrt{3}+3\sqrt{2}\)
\(\sqrt{4-\sqrt{7}}=\frac{\sqrt{2}\sqrt{4-\sqrt{7}}}{\sqrt{2}}=\frac{\sqrt{8-2\sqrt{7}}}{\sqrt{2}}=\frac{\sqrt{7-2\sqrt{7}+1}}{\sqrt{2}}\)
\(=\frac{\sqrt{\left(\sqrt{7}-1\right)^2}}{\sqrt{2}}=\frac{\sqrt{7}-1}{\sqrt{2}}=\frac{\sqrt{14}-\sqrt{2}}{2}\)
\(\sqrt{4+2\sqrt{3}}=\sqrt{3+2\sqrt{3}+1}=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\)
Với \(x\ge1\)thì \(\sqrt{x-2\sqrt{x-1}}=\sqrt{\left(x-1\right)-2\sqrt{x-1}+1}\)
\(=\sqrt{\left(\sqrt{x-1}\right)^2-2\sqrt{x-1}\sqrt{1}+\left(\sqrt{1}\right)^2}\)
\(=\sqrt{\left(\sqrt{x-1}-1\right)^2}=\sqrt{x-1}-1\)
T đã tốn mấy phút cuộc đời viết lời giải cho bạn r, tiếc j mấy giây mà bấm k cho t ik =))
28 tháng 6 2021
`c)(15/(sqrt6+1)+4/(sqrt6-2)-12/(3-sqrt6))*(sqrt6+11)`
`=((15(sqrt6-1))/(6-1)+(4(sqrt6+2))/(6-4)-(12(3+sqrt6))/(9-6))*(sqrt6+11)`
`=(3(sqrt6-1)+2(sqrt6+2)-4(3+sqrt6))*(sqrt6+11)`
`=(3sqrt6-3+2sqrt6+4-12-4sqrt6)*(sqrt6+11)`
`=(sqrt6-11)(sqrt6+11)`
`=6-121=-115`
28 tháng 6 2021
c) Ta có: \(\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right)\left(\sqrt{6}+11\right)\)
\(=\left[3\left(\sqrt{6}-1\right)+2\left(\sqrt{6}+2\right)-4\left(3+\sqrt{6}\right)\right]\left(\sqrt{6}+11\right)\)
\(=\left(3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}\right)\left(\sqrt{6}+11\right)\)
\(=\left(\sqrt{6}-11\right)\left(\sqrt{6}+11\right)\)
=6-121=-115
TH
Thầy Hùng Olm
Manager
VIP
5 tháng 7 2023
a. \(\dfrac{\sqrt{2}.\left(\sqrt{3}+\sqrt{5}\right)}{\sqrt{7}.\left(\sqrt{3}+\sqrt{5}\right)}=\dfrac{\sqrt{2}}{\sqrt{7}}=\sqrt{\dfrac{2}{7}}\)
d. \(\dfrac{\sqrt{6-2\sqrt{5}}}{\sqrt{5}-1}=\dfrac{\sqrt{5-2\sqrt{5}+1}}{\sqrt{5}-1}=\dfrac{\left(\sqrt{5}-1\right)^2}{\sqrt{5}-1}=\sqrt{5}-1\)
DT
10 tháng 6 2019
a)ĐKXĐ \(\orbr{\begin{cases}x\ge3+\sqrt{2}\\x\le3-\sqrt{2}\end{cases}}\)
Đặt \(\sqrt{x^2-6x+7}=a\ge0.\)\(\Rightarrow x^2-6x+7=a^2\Leftrightarrow x^2-6x=a^2-7\)
Ta có phương trình:
\(a^2-7+a=5\Leftrightarrow a^2+a-12=0\Leftrightarrow a^2-3a+4a-12=0\)
\(\Leftrightarrow a\left(a-3\right)+4\left(a-3\right)=0\Leftrightarrow\left(a-3\right)\left(a+4\right)=0\)
\(\Leftrightarrow a-3=0\)(Vì \(a\ge0\rightarrow a+4\ge4\))
\(\Leftrightarrow a=3\Leftrightarrow\sqrt{x^2-6x+7}=3\)
\(\Leftrightarrow x^2-6x+7=9\Leftrightarrow x^2-6x-2=0\)
Ta có \(\Delta^'=3^2-\left(-2\right)=11>0\)
\(\Rightarrow x_1=3-\sqrt{11}\)(TMĐK)
\(x_2=3+\sqrt{11}\)(TMĐK)
Kết luận vậy phương trình đã cho có 2 nghiệm phân biệt .............
b) ĐKXĐ: \(x\ge-1\)
Đặt \(\sqrt{x+1}=a\ge0;\sqrt{x+6}=b>0\)
\(\Rightarrow b^2-a^2=x+6-\left(x+1\right)=5\)
Ta có hệ phương trinh :\(\hept{\begin{cases}a+b=5\\b^2-a^2=5\end{cases}\Leftrightarrow}\hept{\begin{cases}\left(b-a\right)\left(b+a\right)=5\\a+b=5\end{cases}}\Leftrightarrow\hept{\begin{cases}b-a=1\\a+b=5\end{cases}\Leftrightarrow\hept{\begin{cases}a=2\\b=3\end{cases}}}\)(TMĐK)
\(\Leftrightarrow\hept{\begin{cases}\sqrt{x+1}=2\\\sqrt{x+6}=3\end{cases}\Leftrightarrow\hept{\begin{cases}x+1=4\\x+6=9\end{cases}\Leftrightarrow}}x=3\left(TMĐK\right).\)
Vậy phương trình đã cho có nghiệm duy nhất là ...
Chỗ đó bạn viết đề mình không biết vế phải bằng 5 hay 55 nữa
Nếu là 55 thì làm tương tự và chỗ hệ thay bằng \(\hept{\begin{cases}a+b=55\\b^2-a^2=5\end{cases}}\)Giải tương tự tìm được \(\hept{\begin{cases}a=\frac{302}{11}\\b=\frac{303}{11}\end{cases}\Leftrightarrow x=\frac{91083}{121}\left(TMĐK\right).}\)
c) ĐKXĐ \(x\ge1\)
\(\sqrt{x+3-4\sqrt{x-1}}+\sqrt{x+8-6\sqrt{x-1}}=4\)
\(\Leftrightarrow\sqrt{x-1-2.\sqrt{x-1}.2+4}+\sqrt{x-1-2.\sqrt{x-1}.3+9}=4\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(\sqrt{x-1}-3\right)^2}=4\)
\(\Leftrightarrow|\sqrt{x-1}-2|+|\sqrt{x-1}-3|=4\)(3)
* Nếu \(\sqrt{x-1}< 2\)phương trình (3) tương đương với
\(2-\sqrt{x-1}+3-\sqrt{x-1}=4\Leftrightarrow2\sqrt{x-1}=1\)
\(\Leftrightarrow x-1=\frac{1}{4}\Leftrightarrow x=\frac{5}{4}\left(TMĐK\right)\)
* Nếu \(2\le\sqrt{x-1}\le3\)phương trình (3) tương đương với
\(\sqrt{x-1}-2+3-\sqrt{x-1}=4\Leftrightarrow1=4\left(loại\right)\)
* Nếu \(\sqrt{x-1}>3\)phương trình (3) tương đương với
\(\sqrt{x-1}-2+\sqrt{x-1}-3=4\)\(\Leftrightarrow2\sqrt{x-1}=9\Leftrightarrow\sqrt{x-1}=\frac{9}{2}\Leftrightarrow x-1=\frac{81}{4}\Leftrightarrow x=\frac{85}{4}\left(TMĐK\right)\)
Vậy phương trình đã cho có 2 nghiệm phân biệt .......
'
LP
28 tháng 7 2016
a)= \(\frac{\sqrt{2}-1}{2-1}+\frac{\sqrt{3}-\sqrt{2}}{3-2}+...+\frac{\sqrt{100}-\sqrt{99}}{100-99}\)
=\(\sqrt{2}-1+\sqrt{3}-\sqrt{2}+...+\sqrt{100}-\sqrt{99}\)
= \(-1+\sqrt{100}\)
= -1 +10
=9
28 tháng 7 2016
b)Ta có\(\left(\sqrt{n+1}-\sqrt{n}\right)\cdot\left(\sqrt{n+1}+\sqrt{n}\right)\)=n+1-n=1 (1)
Lại có:\(\frac{1}{\sqrt{n+1}+1}\cdot\left(\sqrt{n+1}+1\right)=1\)(2)
Từ (1) và (2)=>\(\left(\sqrt{n+1}-1\right)=\frac{1}{\sqrt{n+1}+1}\)
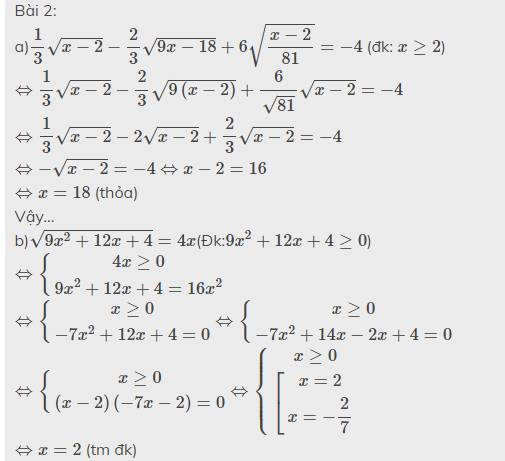
\(\sqrt{21-6\sqrt{6}}=\sqrt{\left(\sqrt{18}\right)^2+2\sqrt{18}\sqrt{3}+\left(\sqrt{3}\right)^2}\)
\(=\sqrt{\left(\sqrt{18}-\sqrt{3}\right)^2}=\sqrt{18}-\sqrt{3}=3\sqrt{2}-\sqrt{3}\)
\(\sqrt{21-6\sqrt{6}}=\sqrt{\left(3\sqrt{2}-\sqrt{3}\right)^2}=3\sqrt{2}-\sqrt{3}\)