
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên
NL
1

MH
15 tháng 11 2021
a + b =150
ƯCLN (a, b) = 5
⇒ a = 5.m trong đó ƯCLN(m, n) = 1 (vì ƯCLN(a,b) = 5)
b = 5.n
⇒⇒ 5m + 5n = 150
5 (m + n) = 150
⇒ m + n = \(\dfrac{150}{5}\) = 30
| m | 29 | 23 | 21 | 19 | 17 |
| n | 1 | 7 | 9 | 11 | 13 |
| a= 5m | 145 | 115 | 105 | 95 | 85 |
| b= 5n | 5 | 35 | 45 | 55 | 65 |
Vậy a có thể bằng 145, 115, 105, 95, 85
b có thể bằng 5, 35, 45, 55, 65


2 tháng 2 2023
Ta có:
A = \(\dfrac{10^7+5}{10^7-8}=\dfrac{10^7-8+13}{10^7-8}=1+\dfrac{13}{10^7-8}\)
\(B=\dfrac{10^8+6}{10^8-7}=\dfrac{10^8-7+13}{10^8-7}=1+\dfrac{13}{10^8-7}\)
Mà \(10^8-7>10^7-8\)
=> \(1+\dfrac{13}{10^7-8}>1+\dfrac{13}{10^8-7}\)
=> A < B
Vậy A < B
2 tháng 2 2023
Xin lỗi mình kết luận sai vì nhìn nhầm. Đáp án đúng là A > B và cả quá trình trên vẫn đúng nha.
NN
1
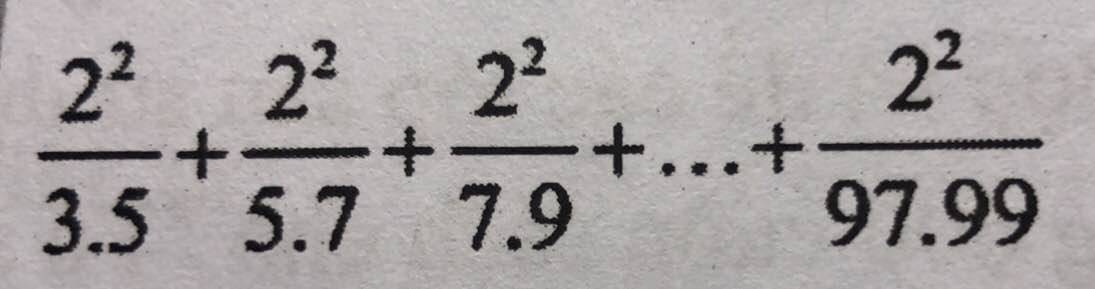
 Mấy bạn giúp mik lẹ zới , cho mik đáp án đầy đủ trong vòng 10phut nha , ( các bạn làm đc bài nào thì làm )
Mấy bạn giúp mik lẹ zới , cho mik đáp án đầy đủ trong vòng 10phut nha , ( các bạn làm đc bài nào thì làm )
\(\dfrac{2^2}{3\cdot5}+\dfrac{2^2}{5\cdot7}+\dfrac{2^2}{7\cdot9}+...+\dfrac{2^2}{97\cdot99}\)
\(=2\dfrac{2}{3\cdot5}+2\dfrac{2}{5\cdot7}+2\dfrac{2}{7\cdot9}+...+2\dfrac{2}{97\cdot99}\)
\(=2\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+...+\dfrac{2}{97\cdot99}\right)\)
\(=2\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{97}-\dfrac{1}{99}\right)\)
\(=2\left(\dfrac{1}{3}-\dfrac{1}{99}\right)\\ =2\cdot\dfrac{32}{99}\\ =\dfrac{64}{99}\)