
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = \(\dfrac{3^{123}+1}{3^{125}+1}\) Vì 3123 + 1 < 2125 + 1 Nên A = \(\dfrac{3^{123}+1}{3^{125}+1}\)< \(\dfrac{3^{123}+1+2}{3^{125}+1+2}\)
A < \(\dfrac{3^{123}+3}{3^{125}+3}\) = \(\dfrac{3.\left(3^{122}+1\right)}{3.\left(3^{124}+1\right)}\) = \(\dfrac{3^{122}+1}{3^{124}+1}\) = B
Vậy A < B


a) Ta có: A = 123 x 123 = 123 x ( 124 - 1 ) = 123 x 124 - 123
B = 121 x 124 = ( 123 - 2 ) x 124 = 123 x 124 - 248
Suy ra: 123 x 124 - 123 > 123 x 124 - 248 hay A > B
b) Ta có: C = 123 x 137137 = 123 x 137 x 1001 = 137 x 123 x 1001
D = 137 x 123123 = 137 x 123 x 1001
Suy ra: C = D
c) Ta có: E = 2015 x 2017 = 2015 x ( 2016 + 1 ) = 2015 x 2016 + 2015
F = 2016 x 2016 = ( 2015 + 1 ) x 2016 = 2015 x 2016 + 2016
Suy ra: 2015 x 2016 + 2015 < 2015 x 2016 + 2016 hay E < F


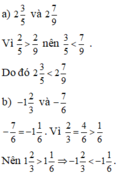
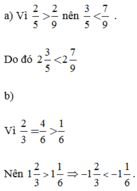

123 + (-3) = 123 – 3= 120. Vậy 123 + (-3) < 123