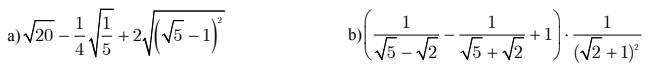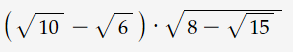K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NB
19 tháng 10 2021
b) \(=\left(5+2\sqrt{3}\right).\sqrt{25-2.5.2\sqrt{3}+12}\\ =\left(5+2\sqrt{3}\right).\sqrt{\left(5-2\sqrt{3}\right)^2}=\left(5+2\sqrt{3}\right).\left(5-2\sqrt{3}\right)=25-12=13\)
19 tháng 10 2021
c: \(\left(2-\dfrac{5-\sqrt{5}}{1-\sqrt{5}}\right)\left(\dfrac{\sqrt{10}+\sqrt{5}}{\sqrt{2}+1}-2\right)\)
\(=\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)\)
=1
23 tháng 6 2021
\(ĐKXĐ:x\ge0;x\ne1;0\)
\(A=\frac{2x+2}{\sqrt{x}}+\frac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\frac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(A=\frac{2x+2}{\sqrt{x}}+\frac{x+\sqrt{x}+1}{\sqrt{x}}-\frac{x-\sqrt{x}+1}{\sqrt{x}}\)
\(A=\frac{2x+2+x+\sqrt{x}+1-x+\sqrt{x}-1}{\sqrt{x}}\)
\(A=\frac{2x+2+2\sqrt{x}}{\sqrt{x}}\)
\(A=2\sqrt{x}+\frac{2}{\sqrt{x}}+2\)
a/d bđt cauchy
\(2\sqrt{x}+\frac{2}{\sqrt{x}}\ge2\sqrt{2.2}=2.2=4\)
\(A\ge4+2=6\)
\(< =>A>5\)
dấu "=" xảy ra khi x=1
30 tháng 8 2021
a, \(\left(\frac{1}{x+2\sqrt{x}}-\frac{1}{\sqrt{x}+2}\right):\frac{1-\sqrt{x}}{x+4\sqrt{x}+4}\)ĐK : x >= 0 ; \(x\ne1\)
\(=\left(\frac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\right).\frac{\left(\sqrt{x}+2\right)^2}{1-\sqrt{x}}=\frac{\sqrt{x}+2}{\sqrt{x}}\)
b, \(F=\frac{5}{2}\Rightarrow\frac{\sqrt{x}+2}{\sqrt{x}}=\frac{5}{2}\Rightarrow2\sqrt{x}+4=5\sqrt{x}\Leftrightarrow3\sqrt{x}=4\Leftrightarrow x=\frac{16}{9}\)
30 tháng 8 2021
ĐK : x > 0 , x khác 1
\(bthuc=\frac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\cdot\frac{\left(\sqrt{x}+2\right)^2}{1-\sqrt{x}}=\frac{\sqrt{x}+2}{\sqrt{x}}\)
Để bthuc = 5/2 thì \(\frac{\sqrt{x}+2}{\sqrt{x}}=\frac{5}{2}\Rightarrow2\sqrt{x}+4=5\sqrt{x}\Leftrightarrow3\sqrt{x}=4\Leftrightarrow x=\frac{16}{9}\left(tm\right)\)
3 tháng 7 2021
\(=\left(\sqrt{5}-\sqrt{3}\right).\sqrt{2}.\sqrt{8-\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right).\sqrt{16-2\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\sqrt{15-2\sqrt{15}+1}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{15}-1\right)^2}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\left|\sqrt{15}-1\right|\)\(=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{15}-1\right)=5\sqrt{3}-\sqrt{5}-3\sqrt{5}+\sqrt{3}\)
\(=6\sqrt{3}-4\sqrt{5}\)
Vậy...
3 tháng 7 2021
\(\left(\sqrt{10}-\sqrt{6}\right)\sqrt{8-\sqrt[]{15}}\)
\(=\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-\sqrt{15}}\)
\(=\sqrt{16-2\sqrt{15}}.\left(\sqrt{5}-\sqrt{3}\right)=\sqrt{\left(\sqrt{15}-1\right)^2}\left(\sqrt{5}-\sqrt{3}\right)\)
\(=\left(\sqrt{15}-1\right)\left(\sqrt{5}-\sqrt{3}\right)=5\sqrt{3}-3\sqrt{5}-\sqrt{5}+\sqrt{3}=6\sqrt{3}-4\sqrt{5}\)
23 tháng 6 2021
a, \(B=\left(\frac{\sqrt{a}+2}{a+2\sqrt{a}+1}-\frac{\sqrt{a}-2}{a-1}\right)\frac{\sqrt{a}+1}{\sqrt{a}}\)ĐKXĐ : \(a>0;a\ne1\)
\(=\left(\frac{\left(\sqrt{a}+2\right)\left(\sqrt{a}-1\right)-\left(\sqrt{a}-2\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)}\right)\frac{\sqrt{a}+1}{\sqrt{a}}\)
\(=\left(\frac{a+\sqrt{a}-2-a+\sqrt{a}+2}{a-1}\right)\frac{1}{\sqrt{a}}\)
\(=\frac{2\sqrt{a}}{\left(a-1\right)\sqrt{a}}=\frac{2}{a-1}\)
b, quá rõ ràng rồi nhé
8 tháng 12 2021
a, \(\dfrac{\sqrt{80}}{\sqrt{5}}\)-\(\sqrt{5}\).\(\sqrt{20}\)= \(\sqrt{16}\)-10=-6
b, (\(\sqrt{28}\)-\(\sqrt{12}\)-\(\sqrt{7}\))\(\sqrt{7}\)+2\(\sqrt{21}\)=\(\sqrt{196}\)-\(\sqrt{84}\)-7+2 \(\sqrt{21}\)=14-7=7
c, \(\sqrt[3]{2}\).\(\sqrt[3]{32}\)+\(\sqrt{2}\).\(\sqrt{32}\)=\(\sqrt[3]{64}\)+\(\sqrt{64}\)=4+8=12
d, \(2\sqrt{8\sqrt{3}}\)-\(\sqrt{2\sqrt{3}}\)-\(\sqrt{9\sqrt{12}}\)=\(4\sqrt{12}\)-\(\sqrt{12}\)-\(3\sqrt{12}\)=0
9 tháng 3 2022
1: Thay x=16 vào A, ta được:
\(A=\dfrac{16-4}{4-2}=\dfrac{12}{2}=6\)
2: \(B=\dfrac{x-4+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}=\dfrac{x-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)