Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P=\dfrac{-2sin5x.sinx-sinx}{2sin5x.cosx+cosx}=\dfrac{-sinx\left(2sin5x+1\right)}{cosx\left(2sin5x+1\right)}=-tanx\)

Chọn B.
Ta có A = sin6x + cos6x + 3sin2x.cos2x.
= ( sin2x)3 + (cos2x)3 + 3sin2x.cos2x.
= (sin2x + cos2x)3 - 3sin2x.cos2x(sin2x + cos2x) + 3.sin2x.cos2x
= 1 - 3.sin2x.cos2x + 3.sin2x.cos2x = 1

Chọn A.
Ta có:
+ sin4x + cos4x = (sin2x + cos2x)2 - 2sin2x.cos2x = 1 - 2sin2x.cos2x.
+ sin4x + cos4x = 1 - 3sin2x.cos2x.
Do đó
A = 3(1 - 2sin2x.cos2x) - 2(1 - 3sin2x.cos2x) = 1.

\(D=\frac{sin4x+sin5x+sin6x}{cos4x+cos5x+cos6x}\)
\(=\frac{\left(sin4x+sin6x\right)+sin5x}{\left(cos4x+cos6x\right)+cos5x}\)
\(=\frac{2sin\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+sin5x}{2cos\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+cos5x}\)
\(=\frac{2sin5x.cos\left(-x\right)+sin5x}{2cos5x.cos\left(-x\right)+cos5x}=\frac{sin5x\left(2.cos\left(-x\right)+1\right)}{cos5x\left(2.cos\left(-x\right)+1\right)}=\frac{sin5x}{cos5x}=tan5x\)

Câu 5. Cho x,y dương thỏa mãn \(x+y=\dfrac{1}{2}\).Tìm giá trị nhỏ nhất của
\(P=\dfrac{1}{x}+\dfrac{1}{y}\)
Giải:
\(P=\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{x+y}{xy}=\dfrac{\dfrac{1}{2}}{xy}=\dfrac{2}{xy}\)
--> P nhỏ nhất khi \(xy\) lớn nhất
Ta có:
\(x^2+y^2\ge2xy\) ( BĐT AM-GM )
\(\Leftrightarrow\left(x+y\right)^2\ge4xy\)
\(\Leftrightarrow1\ge4xy\)
\(\Leftrightarrow xy\le\dfrac{1}{4}\)
\(\Rightarrow P\ge2:\dfrac{1}{4}=8\)
Vậy \(Min_P=8\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{4}\)

Chọn C.
Ta có sin6x + cos6x = ( sin2x + cos2x) 3- 3sin2xcos2x( sin2x + cos2x)
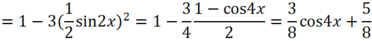
Do đó; m = 3/8 và n = 5/8.
Suy ra S = 0.
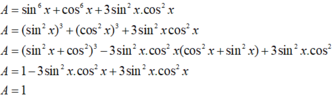
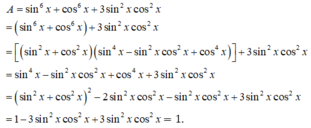

\(P=\dfrac{1+2sin3xcos3x-\left(1-2sin^23x\right)}{1+2sin3xcos3x+2cos^2x-1}=\dfrac{2sin3xcos3x+2sin^23x}{2sin3xcos3x+2cos^23x}=\dfrac{sin3x}{cos3x}=tan3x\)
\(x=\dfrac{7\pi}{4}\Rightarrow P=tan\dfrac{21\pi}{4}=tan\dfrac{\pi}{4}=1\)