Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Ta có : sin4x + cos4x = ( sin2x + cos2x) 2- 2sin2x.cos2x = 1- 2( ½ .sin2x) 2
![]()
Do đó: m = ¼ và n = ¾
Và S = 0.

\(d\left(A;\Delta\right)=\dfrac{\left|-3\left(m-2\right)+9\left(m+1\right)-5m+1\right|}{\sqrt{\left(m-2\right)^2+\left(m+1\right)^2}}\)
\(=\dfrac{\left|m+16\right|}{\sqrt{2m^2-2m+5}}=k\Rightarrow\left(m+16\right)^2=k^2\left(2m^2-2m+5\right)\)
\(\Rightarrow\left(2k^2-1\right)m^2-2\left(k^2+16\right)m+5k^2-256=0\)
\(\Delta'=\left(k^2+16\right)^2-\left(2k^2-1\right)\left(5k^2-256\right)\ge0\)
\(\Rightarrow0\le k^2\le61\) \(\Rightarrow k^2_{max}=61\) khi \(m=\dfrac{7}{11}\)

Đồ thị hàm số đi qua hai điểm M, N nên  suy ra S = a + b = 2
suy ra S = a + b = 2
Chọn C.

Đặt x + 1 t = t , t ≥ 2 khi đó phương trình trở thành 2 t 2 − 3 t − 5 m − 3 = 0 ( * )
Phương trình 2 x 2 + 1 x 2 - 3 x + 1 x - 5 m + 1 = 0 có nghiệm khi và chỉ khi phương trình (*) có nghiệm t thỏa mãn t ≥ 2
Số nghiệm của phương trình (*) bằng số giao điểm của parabol (P): y = 2 t 2 − 3 t − 3 và đường thẳng d : y = 5 m
Xét parabol P : y = 2 t 2 - 3 t - 3 ta có bảng biến thiên như sau:
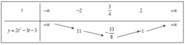
Từ bảng biến thiên ta có phương trình (*) có nghiệm t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ ) khi và chỉ khi 5 m ≥ - 1 hoặc 5 m ≥ 11
![]()
Vậy khi m ∈ − 1 5 ; + ∞ thì phương trình có nghiệm ⇒ a = 1 b = 5 ⇒ T = 5
Đáp án cần chọn là: B

Điều kiện: 3 x 2 + 7 x ≥ 0 3 x − 1 ≥ 0 ⇔ x ≥ 1 3 *
Với điều kiện trên, phương trình tương đương
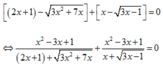
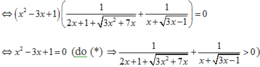
![]()
Theo yêu cầu đề bài ta chọn nghiệm x = 3 + 5 2
Vậy a = 3 , b = 5 , c = 2 ⇒ S = a + b + c = 10
Đáp án cần chọn là: C

a) Vì đồ thị hàm số ax+b song song với (d1) nên a=3
hay hàm số có dạng là y=3x+b
Vì đồ thị hàm số y=3x+b đi qua điểm C(3;-2)
nên Thay x=3 và y=-2 vào hàm số y=3x+b, ta được:
\(3\cdot3+b=-2\)
\(\Leftrightarrow b+9=-2\)
hay b=-11
Vậy: Hàm số có dạng là y=3x-11
b) Vì (d)⊥(d2) nên \(a\cdot4=-1\)
hay \(a=-\dfrac{1}{4}\)
Vậy: Hàm số có dạng là \(y=-\dfrac{1}{4}x+b\)
Vì (d) đi qua D(2;-1) nên
Thay x=2 và y=-1 vào hàm số \(y=-\dfrac{1}{4}x+b\), ta được:
\(-\dfrac{1}{4}\cdot2+b=-1\)
\(\Leftrightarrow b-\dfrac{1}{2}=-1\)
hay \(b=-\dfrac{1}{2}\)
Vậy: \(a=-\dfrac{1}{4}\) và \(b=-\dfrac{1}{2}\)
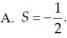
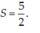

Chọn C.
Ta có sin6x + cos6x = ( sin2x + cos2x) 3- 3sin2xcos2x( sin2x + cos2x)
Do đó; m = 3/8 và n = 5/8.
Suy ra S = 0.