Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1:
a: \(\left(2x-5\right)^2-4x\left(x+3\right)\)
\(=4x^2-20x+25-4x^2-12x\)
=-32x+25
b: \(\left(x-2\right)^3-6\left(x+4\right)\left(x-4\right)-\left(x-2\right)\left(x^2+2x+4\right)\)
\(=x^3-6x^2+12x-8-\left(x^3-8\right)-6\left(x^2-16\right)\)
\(=-6x^2+12x-6x^2+96=-12x^2+12x+96\)
c: \(\left(x-1\right)^2-2\left(x-1\right)\left(x+2\right)+\left(x+2\right)^2+5\left(2x-3\right)\)
\(=\left(x-1-x-2\right)^2+5\left(2x-3\right)\)
\(=\left(-3\right)^2+5\left(2x-3\right)\)
\(=9+10x-15=10x-6\)
2:
a: \(\left(2-3x\right)^2-5x\left(x-4\right)+4\left(x-1\right)\)
\(=9x^2-12x+4-5x^2+20x+4x-4\)
\(=4x^2+12x\)
b: \(\left(3-x\right)\left(x^2+3x+9\right)+\left(x-3\right)^3\)
\(=27-x^3+x^3-9x^2+27x-27\)
\(=-9x^2+27x\)
c: \(\left(x-4\right)^2\left(x+4\right)-\left(x-4\right)\left(x+4\right)^2+3\left(x^2-16\right)\)
\(=\left(x-4\right)\left(x+4\right)\left(x-4-x-4\right)+3\left(x^2-16\right)\)
\(=\left(x^2-16\right)\left(-8\right)+3\left(x^2-16\right)\)
\(=-5\left(x^2-16\right)=-5x^2+80\)

\(a,-5x\left(x-3\right)\left(2x+4\right)-\left(x+3\right)\left(x-3\right)+\left(5x-2\right)\left(3x+4\right)\)
\(=-5x\left(2x^2-x-12\right)-\left(x^2-9\right)+15x^2+20x-6x-8\)
\(=-10x^3+5x^2+60x-x^2+9+15x^2+20x-6x-8\)
\(=-10x^3+19x^2+74x+1\)
\(b,\left(4x-1\right)x\left(3x+1\right)-5x^2.x\left(x-3\right)-\left(x-4\right)x\left(x-5\right)\)\(-7\left(x^3-2x^2+x-1\right)\)
\(=\left(4x^2-x\right)\left(3x+1\right)-5x^4-15x^3-\left(x^2-4x\right)\left(x-5\right)\)\(-7x^3+14x^2-7x+7\)
\(=12x^3+x^2-x-5x^4-15x^3-x^3+9x^2+20x\)\(-7x^3+14x^2-7x+7\)
\(=-5x^4-11x^3+24x^2+12x+7\)
\(c,\left(5x-7\right)\left(x-9\right)-\left(3-x\right)\left(2-5x\right)-2x\left(x-4\right)\)
\(=5x^2-52x+63-6+17x-5x^2-2x^2+8x\)
\(=-2x^2-27x+57\)
\(d,\left(5x-4\right)\left(x+5\right)-\left(x+1\right)\left(x^2-6\right)-5x+19\)
\(=5x^2+21x-20-x^3-x^2+6x+6-5x+19\)
\(=-x^3+4x^2+22x+5\)
\(e,\left(9x^2-5\right)\left(x-3\right)-3x^2\left(3x+9\right)-\left(x-5\right)\left(x+4\right)-9x^3\)
\(=9x^3-27x^2-5x+15-9x^3-27x^2-x^2+x+20-9x^3\)
\(=-9x^3-55x^2+4x+35\)
\(g,\left(x-1\right)^2-\left(x+2\right)^2\)
\(=x^2-2x+1-x^2-4x-4\)
\(=-6x-3\)

1: Ta có: \(x^2-2x+5-\left(x-7\right)\left(x+2\right)\)
\(=x^2-2x+5-x^2-2x+7x-14\)
\(=3x-9\)
2: Ta có: \(-5x\left(x-5\right)+\left(x-3\right)\left(x^2-7\right)\)
\(=-5x^2+25x+x^3-7x-3x^2+21\)
\(=x^3-8x^2+18x+21\)
3: Ta có: \(x\left(x^2-x-2\right)-\left(x+5\right)\left(x-1\right)\)
\(=x^3-x^2-2x-x^2-4x+5\)
\(=x^3-2x^2-6x+5\)

\(F=-3\left(x-8\right)\left(2x+1\right)-\left(x+5\right)\left(2-3x\right)-4x\left(x-6\right)\)
\(=-3\left(-3-8\right)\left(-6+1\right)-\left(5-3\right)\left(2+9\right)+12\left(-9\right)\)
\(=-3\left(-11\right)\left(-5\right)-\left(-2\right)11-12.9\)
\(=-165+22-108=22-273=-251\)
\(G=\left(5x-4\right)\left(5-2x\right)-7x\left(x^2-4x+3\right)+\left(x^2-4x\right)\left(7x-2\right)\)
\(=\left(5-4\right)\left(5-2\right)-7\left(1-4+3\right)+\left(1-4\right)\left(7-2\right)\)
\(=3-7.0+5.\left(-3\right)=3-15=-12\)
\(H=\left(-3x+5\right)\left(x-6\right)-\left(x-1\right)\left(x^2-2x+3\right)+\left(x+2\right)\left(x^2-3\right)\)
\(=\left(3+5\right)\left(-1-6\right)-\left(-1-1\right)\left(1+2+3\right)+\left(-1+2\right)\left(1-3\right)\)
\(=8\left(-7\right)-\left(-2\right)6+1\left(-2\right)=-56+12-2=-46\)
\(L=5x\left(x-1\right)\left(2x+3\right)-10x\left(x^2-4x+5\right)-\left(x-1\right)\left(x-4\right)\)
\(=-\frac{5}{3}\left(-\frac{4}{3}\right)\left(-\frac{2}{3}+3\right)+\frac{10}{3}\left(\frac{1}{9}+\frac{4}{3}+5\right)-\left(-\frac{4}{3}\right)\left(-\frac{1}{3}-4\right)\)
\(=\frac{20}{9}\left(\frac{7}{3}\right)+\frac{10}{3}\left(\frac{13}{9}+5\right)+\frac{4}{3}\left(-\frac{13}{3}\right)\)
\(=\frac{140}{27}+\frac{10}{3}.\frac{58}{9}-\frac{52}{9}\)
\(=\frac{140}{27}+\frac{580}{27}-\frac{156}{27}=\frac{140+580-156}{27}=\frac{720-156}{27}=\frac{564}{27}\)
\(M=-7x\left(x-5\right)-\left(x-1\right)\left(x^2-x-2\right)+x^2\left(x-3\right)-5x\left(x-8\right)\)
\(=\frac{-7}{2}\left(\frac{1}{2}-5\right)+\frac{\left(\frac{1}{4}-\frac{1}{2}-2\right)}{2}+\frac{1}{4}\left(\frac{1}{2}-3\right)-\frac{5}{2}\left(\frac{1}{2}-8\right)\)
\(=\frac{7}{2}.\frac{9}{2}-\frac{9}{8}-\frac{1}{4}.\frac{5}{2}+\frac{5}{2}.\frac{15}{2}\)
\(=\frac{63}{4}-\frac{9}{8}-\frac{5}{8}+\frac{75}{4}=\frac{138}{4}-\frac{7}{4}=\frac{131}{4}\)

1: \(=6x^2+2x-15x-5-x^2+6x-9+4x^2+20x+25-27x^3-27x^2-9x-1\)
=-27x^3-18x^2+4x+10
2: =4x^2-1-6x^2-9x+4x+6-x^3+3x^2-3x+1+8x^3+36x^2+54x+27
=7x^3+37x^2+46x+33
5:
\(=25x^2-1-x^3-27-4x^2-16x-16-9x^2+24x-16+\left(2x-5\right)^3\)
\(=8x^3-60x^2+150-125+12x^2-x^3+8x-60\)
=7x^3-48x^2+8x-35

7: Ta có: \(\left(3x+4\right)\left(2x-1\right)+6x\left(1-x\right)=0\)
\(\Leftrightarrow6x^2-3x+8x-4+6x-6x^2=0\)
\(\Leftrightarrow11x=4\)
hay \(x=\dfrac{4}{11}\)
8: Ta có: \(2x\left(x^2-1\right)+x\left(-2x^2-3x+1\right)=-x-27\)
\(\Leftrightarrow2x^3-2x-2x^3-3x^2+x+x+27=0\)
\(\Leftrightarrow x^2=9\)
hay \(x\in\left\{3;-3\right\}\)

Bài 1
A= (x-2)(2x-1)-2x(x+3)=2x2-x-4x+2-2x2-6x=-11x+2
Bài 1:
a) \(A=\left(x-2\right)\left(2x-1\right)-2x\left(x+3\right)\)
\(A=2x^2-x-4x+2-2x^2-6x\)
\(A=-11x+2\)
b) \(B=\left(3x-2\right)\left(2x+1\right)-\left(6x-1\right)\left(x+2\right)\)
\(B=6x^2+3x-4x-2-6x^2-12x+x+2\)
\(B=-12x\)
c) \(C=6x\left(2x+3\right)-\left(4x-1\right)\left(3x-2\right)\)
\(C=12x^2+18x-12x^2+8x+3x-2\)
\(C=29x-2\)
d) \(D=\left(2x+3\right)\left(5x-2\right)+\left(x+4\right)\left(2x-1\right)-6x\left(2x-3\right)\)
\(D=10x^2-4x+15x-6+2x^2-x+8x-4-12x^2+18x\)
\(D=36x-10\)
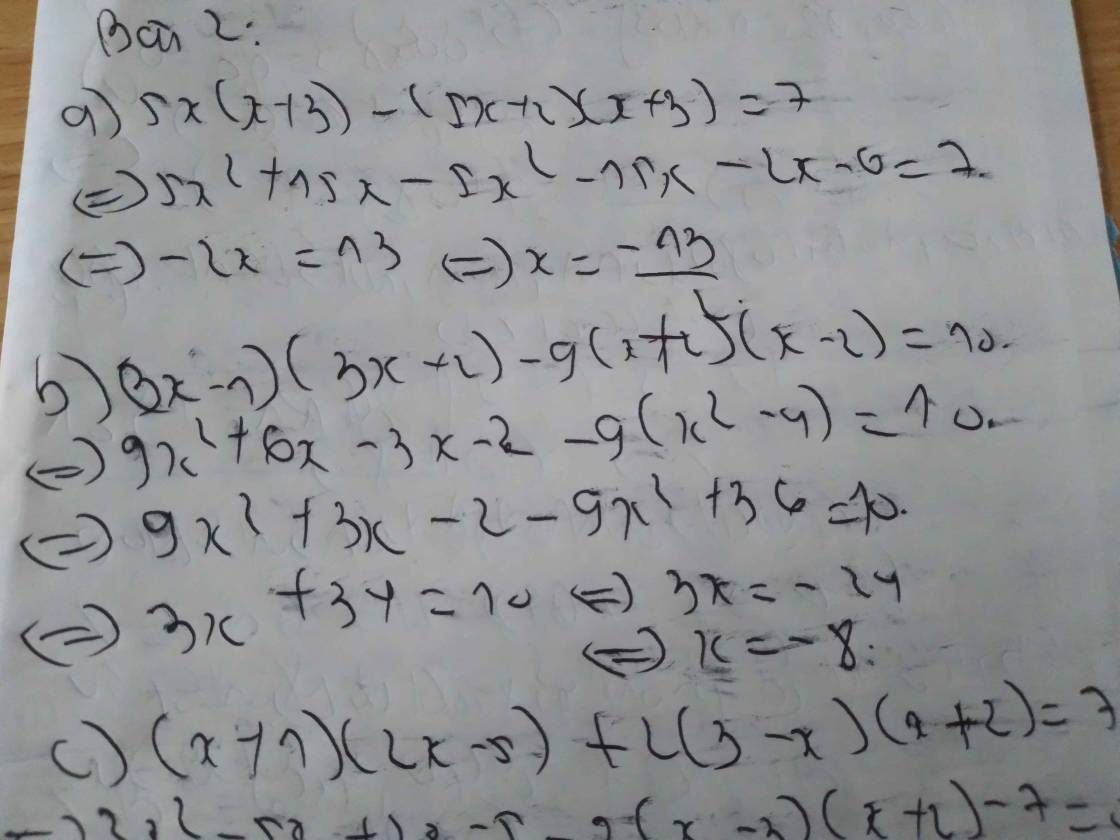


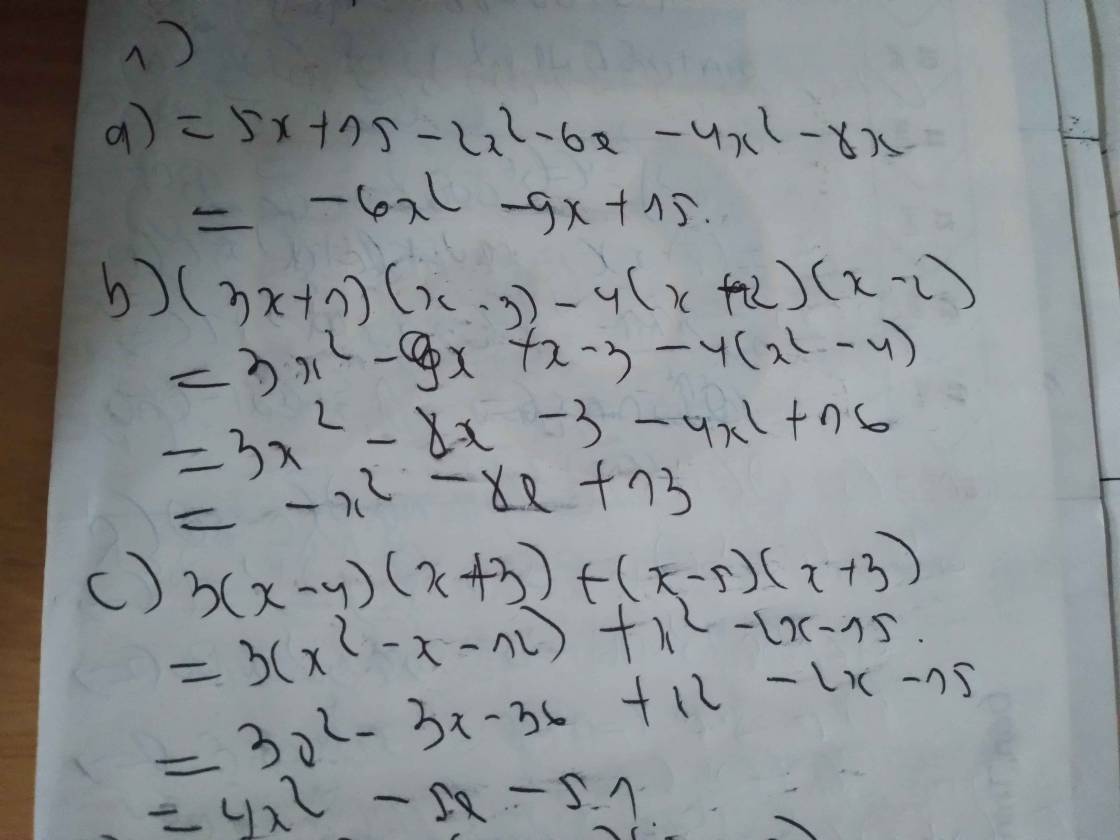
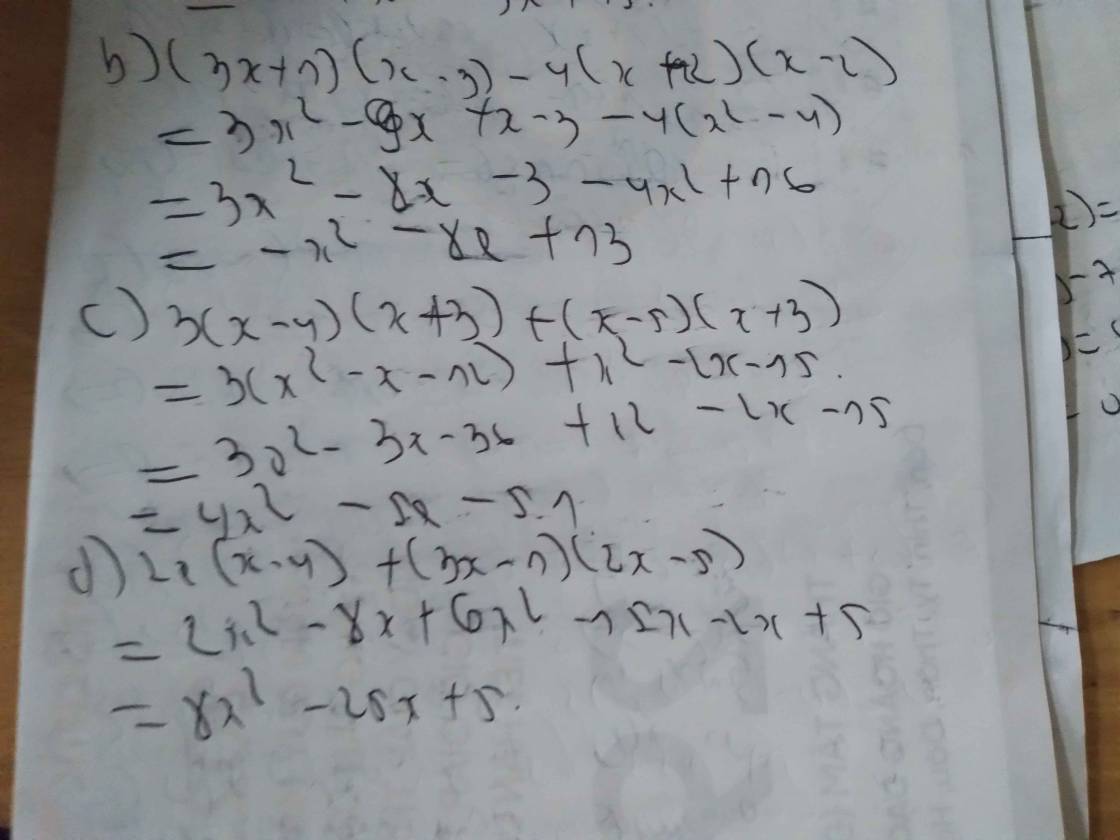
a)\(\left(x-3\right)\left(x+3\right)\left(x+2\right)-\left(x-1\right)\left(x^2-3\right)-5x\left(x+4\right)^2-\left(x-5\right)^2\)
\(=\left(x^2-9\right)\left(x+2\right)-\left(x^3-3x-x^2+3\right)-5x\left(x^2+8x+16\right)-\left(x^2-10x+25\right)\)
\(=x^3+2x^2-9x-18-x^3+x^2+3x-3-5x^3-40x^2-80x-x^2+10x-25\)
\(=-5x^3-38x^2-76x-46\)
b)\(2x\left(x-4\right)^2-\left(x+5\right)\left(x-2\right)\left(x+2\right)+2\left(x+5\right)^2-\left(x-1\right)^2\)
\(=2x\left(x^2-8x+16\right)-\left(x+5\right)\left(x^2-4\right)+2\left(x^2+10x+25\right)-\left(x^2-2x+1\right)\)
\(=2x^3-16x^2+32x-\left(x^3+5x^2-4x-20\right)+2x^2+20x+50-x^2+2x-1\)
\(=x^3-20x^2+58x+69\)
c)\(\left(x+5\right)^2-4x\left(2x+3\right)^2-\left(2x-1\right)\left(x+3\right)\left(x-3\right)\)
\(=x^2+10x+25-4x\left(4x^2+12x+9\right)-\left(2x-1\right)\left(x^2-9\right)\)
\(=x^2+10x+25-16x^3-48x^2-36x-\left(2x^3-x^2-18x+9\right)\)
\(=-18x^3-46x^2-8x+16\).
a) Ta có: \(\left(x-3\right)\left(x+3\right)\left(x+2\right)-\left(x-1\right)\left(x^2-3\right)-5x\left(x+4\right)^2-\left(x-5\right)^2\)
\(=\left(x^2-9\right)\left(x+2\right)-\left(x-1\right)\left(x^2-3\right)-5x\left(x^2+8x+16\right)-\left(x^2-10x+25\right)\)
\(=x^3+2x^2-9x-18-\left(x^3-3x-x^2+3\right)-5x^3-40x^2-80x-x^2+10x-25\)
\(=-4x^3-39x^2-79x-43-x^3+3x+x^2-3\)
\(=-5x^3-38x^2-76x-46\)
b) Ta có: \(2x\left(x-4\right)^2-\left(x+5\right)\left(x-2\right)\left(x+2\right)+2\left(x+5\right)^2-\left(x-1\right)^2\)
\(=2x\left(x^2-8x+16\right)-\left(x+5\right)\left(x^2-4\right)+2x^2+20x+50-x^2+2x-1\)
\(=2x^3-16x^2+32x-x^3+4x-5x^2+20+x^2+22x+49\)
\(=x^3-20x^2+56x+49\)
c) Ta có: \(\left(x+5\right)^2-4x\left(2x+3\right)^2-\left(2x-1\right)\left(x-3\right)\left(x+3\right)\)
\(=x^2+10x+25-4x\left(4x^2+12x+9\right)-\left(2x-1\right)\left(x^2-9\right)\)
\(=x^2+10x+25-16x^3+48x-36x-2x^3+18x+x^2-9\)
\(=-18x^3+2x^2+40x+16\)