Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta chứng minh khẳng định đúng với mọi n ε N* , n ≥ 4.
Với n = 4, ta có tứ giác nên nó có hai đường chéo.
Mặt khác thay n = 4 vào công thức, ta có số đường chéo của tứ giác theo công thức là: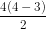 
= 2
Vậy khẳng định là đúng với n= 4.
Giả sử khẳng định là đúng với n = k ≥ 4, tức là đa giác lồi k cạnh có
số đường chéo là 
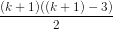
đường chéo (giả thiết quy nạp). Nối Ak+1 với các đỉnh A2, A3, …, Ak-1, ta được thêm k -2 đường chéo, ngoài ra A1Ak cũng là một đường chéo.Vậy số đường chéo của đa giác k + 1 cạnh là
+ k - 2 + 1 =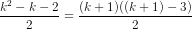 
Như vậy, khẳng định cũng đúng với đa giác k + 1 cạnh
Xét 1 đỉnh bất kì nối tới 17 đỉnh (trừ ra 2 đỉnh kề với đỉnh đang xét) ta đc 17 đường chéo.
Có 20 đỉnh suy ra có :
20.17=340 (đường chéo)
Nhưng như thế mỗi đường chéo ta đã được tính 2 lần .
Vậy số đường chéo trong 1 đa giác lồi 20 cạnh là :
340 : 2=170 (đường chéo)
Xét 1 đỉnh bất kì nối tới 17 đỉnh (trừ ra 2 đỉnh kề với đỉnh đang xét) ta được 17 đường chéo.
Có 20 đỉnh suy ra có 20 . 17 = 340 đường chéo.
Nhưng như thế mỗi đường chéo ta đã kể 2 lần.
Vậy số đường chéo trong 1 đa giác lồi 20 cạnh là \(\dfrac{340}{2}\) = 170 đường chéo.
Số vecto tạo bởi các đỉnh của đa giác: \(A_n^2=\frac{n!}{\left(n-2\right)!}=n\left(n-1\right)\)
Số đường chéo của đa giác: \(\frac{n\left(n-3\right)}{2}\)
\(\Rightarrow n\left(n-1\right)=3n\left(n-3\right)\)
\(\Rightarrow n-1=3n-9\Rightarrow n=4\)
Đáp án D
Cứ 2 điểm k liền kề nhau sẽ tạo thành 1 đường chéo
Vậy số đường chéo là:
C
10
2
-
10
=
45
-
10
=
35
Đa giác lồi n cạnh có n đỉnh.
Chọn 2 điểm bất kì trong số các đỉnh của một đa giác ta được 1 cạnh hoặc 1 đường chéo của đa giác.
⇒Tổng số cạnh và đường chéo của đa giác bằng:
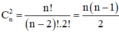
⇒ số đường chéo của đa giác lồi có n cạnh là:
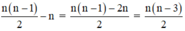
Đáp án là C
Đa giác lồi 10 cạnh thì có 10 đỉnh.
Lấy hai điểm bất kỳ trong 10 đỉnh của đa giác lồi ta được số đoạn thẳng gồm cạnh và đường chéo của đa giác lồi.
Do đó, tổng số cạnh và đường chéo của đa giác là: C 2 10
Suy ra,số đường chéo cần tìm là C 10 2 - 10 = 10 ! 8 ! . 2 ! - 10 = 35