K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 7 2018
a) \(\dfrac{14}{2\sqrt{3}-\sqrt{5}}\)
\(=\dfrac{14\left(2\sqrt{3}+\sqrt{5}\right)}{\left(2\sqrt{3}-\sqrt{5}\right)\left(2\sqrt{3}+\sqrt{5}\right)}\)
\(=\dfrac{14\left(2\sqrt{3}+\sqrt{5}\right)}{\left(2\sqrt{3}\right)^2-\sqrt{5^2}}=\dfrac{14\left(2\sqrt{3}+\sqrt{5}\right)}{12-5}\)
\(=\dfrac{14\left(2\sqrt{3}+\sqrt{5}\right)}{7}=2\left(2\sqrt{3}+\sqrt{5}\right)\)
\(=4\sqrt{3}+2\sqrt{5}\)
b) \(\dfrac{x^2-y}{x-\sqrt{y}}=\dfrac{\left(x-\sqrt{y}\right)\left(x+\sqrt{y}\right)}{x-\sqrt{y}}=x+\sqrt{y}\)
DT
1
14 tháng 9 2017
\(\frac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}=\frac{\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)}{2}\)
PL
0
XT
1
12 tháng 8 2018
mấy bài dạng này bn nên sử dụng cách nhân liên hợp hoặc phân tích đa thức thành nhân tử nha . mk lm 1 bài còn lại thì bn tự lm cho quen nha :)
a) ta có : \(\dfrac{\sqrt{6}+\sqrt{14}}{2\sqrt{3}-\sqrt{7}}=\dfrac{\left(\sqrt{6}+\sqrt{14}\right)\left(2\sqrt{3}+\sqrt{7}\right)}{\left(2\sqrt{3}-\sqrt{7}\right)\left(2\sqrt{3}+\sqrt{7}\right)}\)
\(=\dfrac{6\sqrt{2}+\sqrt{42}+2\sqrt{42}+7\sqrt{2}}{\left(2\sqrt{3}\right)^2-\left(\sqrt{7}\right)^2}=\dfrac{13\sqrt{2}+3\sqrt{42}}{5}\)
gợi ý : b) phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức số \(6\)
c) nhân liên hợp 2 lần nha .
AY
12 tháng 8 2018
a) \(\dfrac{\sqrt{6}+\sqrt{14}}{2\sqrt{3}-\sqrt{7}}\)
=\(\dfrac{\left(\sqrt{6}+\sqrt{14}\right)\left(2\sqrt{3}+\sqrt{7}\right)}{\left(2\sqrt{3}-\sqrt{7}\right).\left(2\sqrt{3}+\sqrt{7}\right)}\)
=\(\dfrac{\left(\sqrt{6}+\sqrt{14}\right).\left(2\sqrt{3}+\sqrt{7}\right)}{12-7}\)
=\(\dfrac{2\sqrt{18}+\sqrt{42}+2\sqrt{42}+\sqrt{98}}{5}\)
=\(\dfrac{6\sqrt{2}+\sqrt{42}+2\sqrt{42}+7\sqrt{2}}{5}\)
=\(\dfrac{3\sqrt{42}+13\sqrt{2}}{5}\)
b) \(\dfrac{5\sqrt{5}+3\sqrt{3}}{\sqrt{5}+\sqrt{3}}\)
=\(\dfrac{\left(5\sqrt{5}+3\sqrt{3}\right).\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}+\sqrt{3}\right).\left(\sqrt{5}-\sqrt{3}\right)}\)
=\(\dfrac{25-5\sqrt{15}+3\sqrt{15}-9}{2}\)
=\(\dfrac{16-2\sqrt{15}}{2}=8-\sqrt{15}\)
Câu c mk chưa làm được
LC
2
24 tháng 8 2023
a: \(\dfrac{6}{5\sqrt{8}}=\dfrac{6}{10\sqrt{2}}=\dfrac{3}{5\sqrt{2}}=\dfrac{3\sqrt{2}}{10}\)
b: \(\dfrac{7}{5+2\sqrt{3}}=\dfrac{7\left(5-2\sqrt{3}\right)}{13}\)
c: \(\dfrac{6}{\sqrt{7}-\sqrt{5}}=\dfrac{6\left(\sqrt{7}+\sqrt{5}\right)}{2}=3\left(\sqrt{7}+\sqrt{5}\right)\)
H9
HT.Phong (9A5)
CTVHS
24 tháng 8 2023
a) \(\dfrac{6}{5\sqrt{8}}\)
\(=\dfrac{6}{5\cdot2\sqrt{2}}\)
\(=\dfrac{6}{10\sqrt{2}}\)
\(=\dfrac{3\sqrt{2}}{5\sqrt{2}\cdot\sqrt{2}}\)
\(=\dfrac{3\sqrt{2}}{10}\)
b) \(\dfrac{7}{5+2\sqrt{3}}\)
\(=\dfrac{7\left(5-2\sqrt{3}\right)}{\left(5+2\sqrt{3}\right)\left(5-2\sqrt{3}\right)}\)
\(=\dfrac{7\left(5-2\sqrt{3}\right)}{5^2-\left(2\sqrt{3}\right)^2}\)
\(=\dfrac{7\left(5-2\sqrt{3}\right)}{13}\)
\(=\dfrac{35-14\sqrt{3}}{13}\)
c) \(\dfrac{6}{\sqrt{7}-\sqrt{5}}\)
\(=\dfrac{6\left(\sqrt{7}+\sqrt{5}\right)}{\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)}\)
\(=\dfrac{6\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=3\sqrt{7}+3\sqrt{5}\)
2 tháng 12 2019
\(\frac{2}{\sqrt{3}-5}=\frac{2\left(\sqrt{3}+5\right)}{3-5^2}=\frac{2\left(\sqrt{3}+5\right)}{-22}=\frac{-5-\sqrt{3}}{11}\)
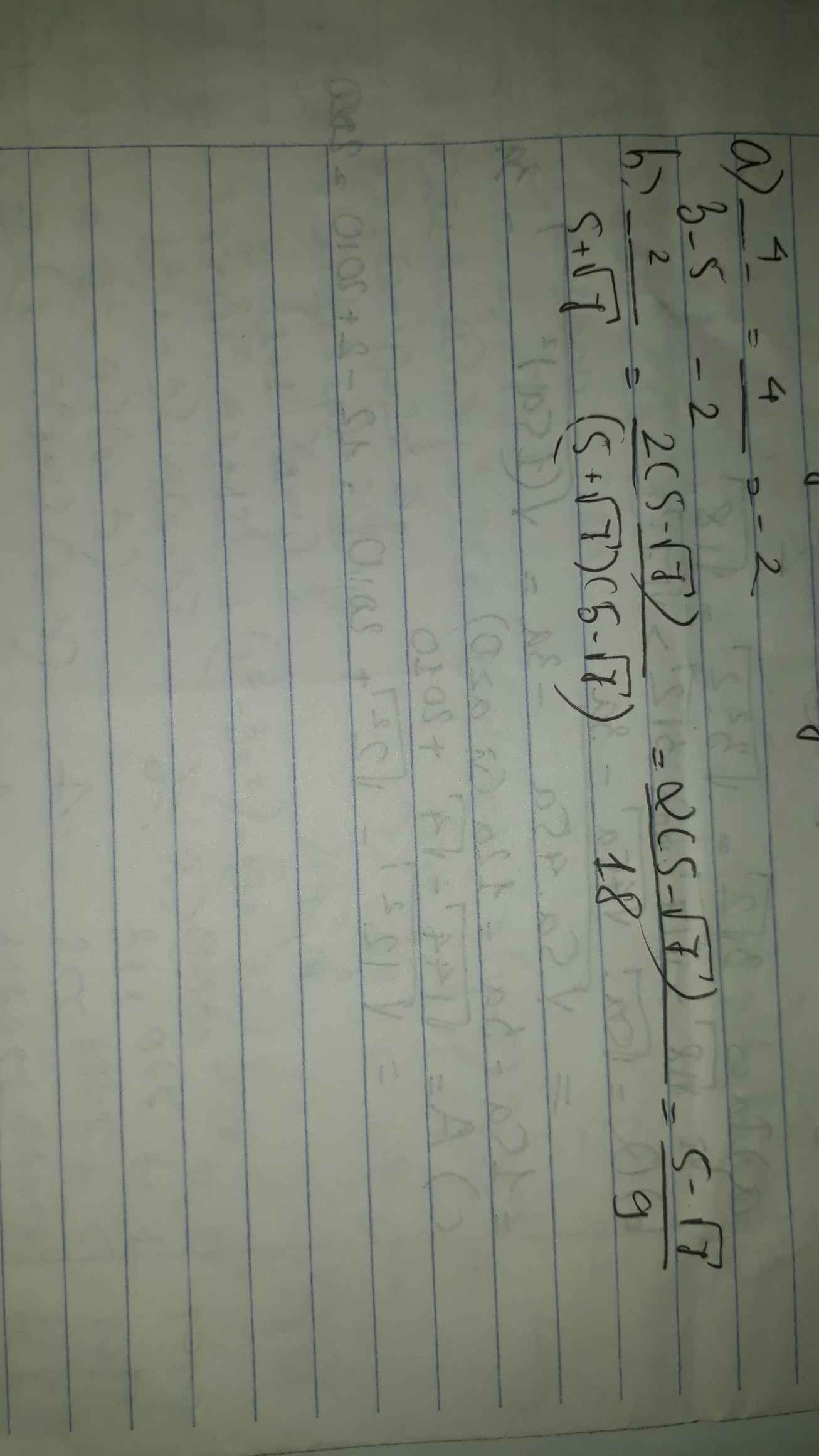
\(=\frac{6\sqrt{2}\left(3\sqrt{7}-5\sqrt{2}\right)}{2\left(3\sqrt{7}-5\sqrt{2}\right)}=\frac{6\sqrt{2}}{2}=3\sqrt{2}\)