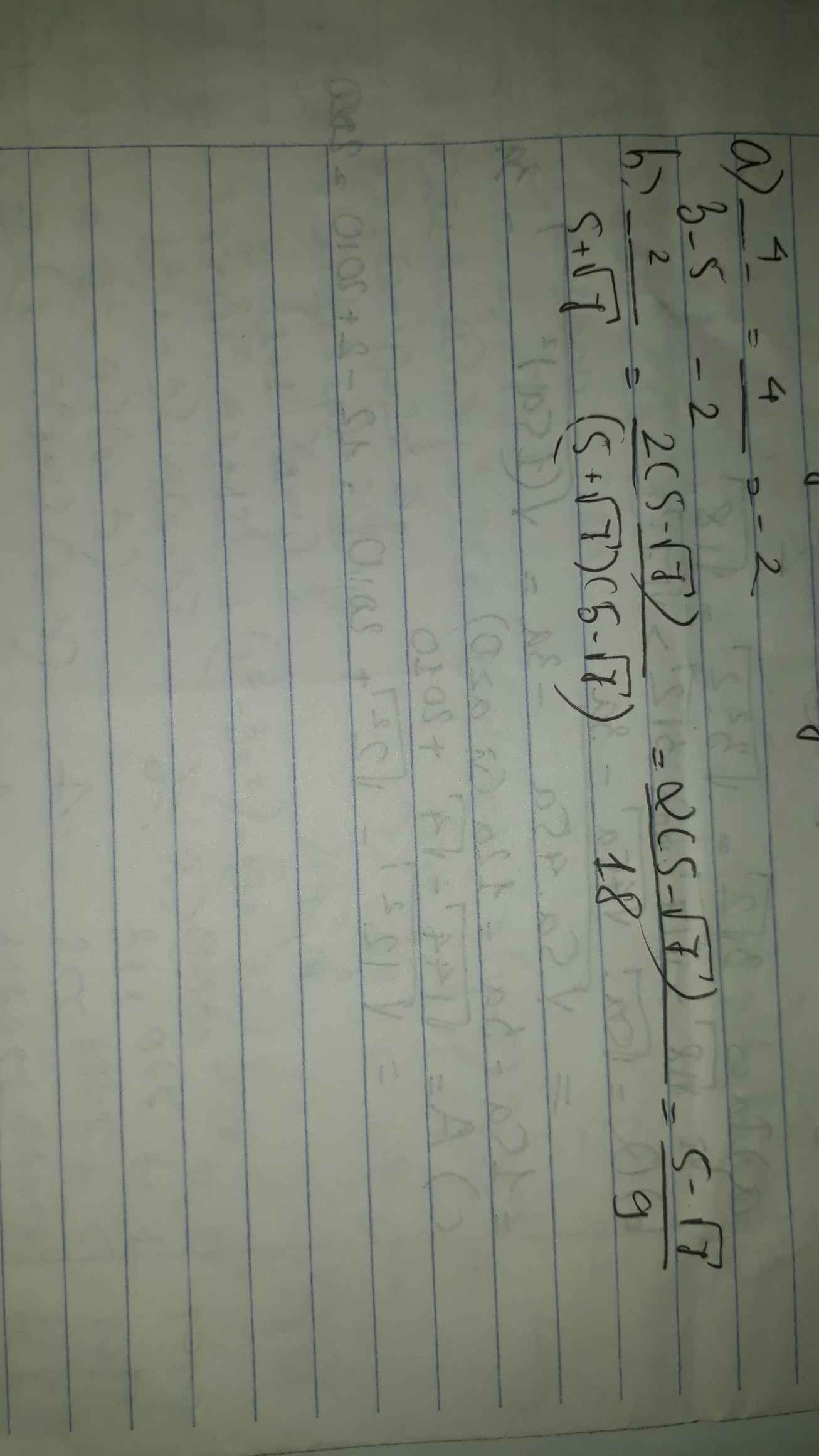Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}=\dfrac{\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)}{\sqrt{2}.\sqrt{2}}=\dfrac{\sqrt{10}-\sqrt{6}}{2}\)
\(\dfrac{1}{\sqrt{3}+\sqrt{2}+1}=\dfrac{\sqrt{3}-\sqrt{2}-1}{\left(\sqrt{3}+\sqrt{2}+1\right)\left(\sqrt{3}-\sqrt{2}-1\right)}\)
\(=\dfrac{\sqrt{3}-\sqrt{2}-1}{3-\left(\sqrt{2}+1\right)^2}=\dfrac{\sqrt{3}-\sqrt{2}-1}{-2\sqrt{2}}=\dfrac{\left(\sqrt{3}-\sqrt{2}-1\right)\sqrt{2}}{-2\sqrt{2}.\sqrt{2}}=\dfrac{\sqrt{6}-2-\sqrt{2}}{-4}\)
\(=\dfrac{2+\sqrt{2}-\sqrt{6}}{4}\)
\(\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}=\dfrac{\sqrt{10}-\sqrt{6}}{2}\)
\(\dfrac{1}{\sqrt{3}+\sqrt{2}+1}=\dfrac{2+\sqrt{2}-\sqrt{6}}{4}\)

Trục căn thức ở mẫu của biểu thức sau :
1 phần 1 cộng căn bậc hai cộng căn bậc ba (sr mik ko bt viết)


\(\dfrac{4}{\sqrt{5}-\sqrt{2}}+\dfrac{3}{\sqrt{5}-2}-\dfrac{2}{\sqrt{3}-2}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{4\left(\sqrt{2}+\sqrt{5}\right)}{\left(\sqrt{5}-\sqrt{2}\right)\left(\sqrt{2}+\sqrt{5}\right)}+\dfrac{3\left(\sqrt{5}+2\right)}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}-\dfrac{2\left(\sqrt{3}+2\right)}{\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{4\left(\sqrt{2}+\sqrt{5}\right)}{\left(\sqrt{5}\right)^2-\left(\sqrt{2}\right)^2}+\dfrac{3\left(\sqrt{5}+2\right)}{\left(\sqrt{5}\right)^2-2^2}-\dfrac{2\left(\sqrt{3}+2\right)}{\left(\sqrt{3}\right)^2-2^2}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{4\left(\sqrt{2}+\sqrt{5}\right)}{3}+\dfrac{3\left(\sqrt{5}+2\right)}{1}-\dfrac{2\left(\sqrt{3}+2\right)}{-1}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{8\left(\sqrt{2}+\sqrt{5}\right)}{6}+\dfrac{18\left(\sqrt{5}+2\right)}{6}+\dfrac{12\left(\sqrt{3}+2\right)}{6}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{8\sqrt{2}+8\sqrt{5}+18\sqrt{5}+36+12\sqrt{3}+24-\sqrt{3}+1}{6}\)
\(=\dfrac{8\sqrt{2}+26\sqrt{5}+11\sqrt{3}+61}{6}\)
\(=\dfrac{4\left(\sqrt{5}+\sqrt{2}\right)}{3}+\dfrac{3\left(\sqrt{5}+2\right)}{1}+\dfrac{2\left(2+\sqrt{3}\right)}{1}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{4\sqrt{5}+4\sqrt{2}+9\sqrt{5}+18}{3}+\dfrac{4+2\sqrt{3}}{1}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{2\left(13\sqrt{5}+4\sqrt{2}+18\right)+24+12\sqrt{3}-\sqrt{3}+1}{6}\)
\(=\dfrac{26\sqrt{5}+4\sqrt{2}+36+25+11\sqrt{3}}{6}\)
\(=\dfrac{61+11\sqrt{3}+26\sqrt{5}+4\sqrt{2}}{6}\)

1) Ta có: \(3\sqrt{12}+\dfrac{1}{2}\sqrt{48}-\sqrt{27}\)
\(=3\cdot2\sqrt{3}+\dfrac{1}{2}\cdot4\sqrt{3}-3\sqrt{3}\)
\(=6\sqrt{3}+2\sqrt{3}-3\sqrt{3}\)
\(=5\sqrt{3}\)
2) Ta có: \(\dfrac{2}{\sqrt{3}-5}\)
\(=\dfrac{2\left(\sqrt{3}+5\right)}{\left(\sqrt{3}-5\right)\left(\sqrt{3}+5\right)}\)
\(=\dfrac{2\left(\sqrt{3}+5\right)}{3-25}\)
\(=\dfrac{-2\left(\sqrt{3}+5\right)}{22}\)
\(=\dfrac{-\sqrt{3}-5}{11}\)
3) Ta có: \(\sqrt{\dfrac{2}{5}}\)
\(=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(=\dfrac{\sqrt{2}\cdot\sqrt{5}}{5}\)
\(=\dfrac{\sqrt{10}}{5}\)
Nếu em thấy các câu hỏi do lag mà bị gửi đúp (tức là rất nhiều câu hỏi giống nhau xuất hiện cùng 1 chỗ) thì xóa giúp mình nhé cho đỡ vướng. Nhưng nhớ để lại 1 câu. Cảm ơn em.


\(\frac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}=\frac{\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)}{2}\)

\(\frac{1}{1-\sqrt[3]{2}}=\frac{\left(1+\sqrt[3]{2}+\sqrt[3]{4}\right)}{\left(1-\sqrt[3]{2}\right)\left(1+\sqrt[3]{2}+\sqrt[3]{4}\right)}=\frac{1+\sqrt[3]{2}+\sqrt[3]{4}}{-1}\)
\(=-1-\sqrt[3]{2}-\sqrt[3]{4}\)
\(=\frac{\left(\sqrt[3]{2^2}+\sqrt[3]{2}+1\right)}{\left(1-\sqrt[3]{2}\right)\left(\left(\sqrt[3]{2^2}+\sqrt[3]{2}+1\right)\right)}\)
=\(\frac{\left(\sqrt[3]{2^2}+\sqrt[3]{2}+1\right)}{1-2}\)
\(-\left(\sqrt[3]{2^2}+\sqrt[3]{2}+1\right)\)

\(a,\frac{\sqrt{5}}{\sqrt{3-\sqrt{5}}}=\frac{\sqrt{5}\left(\sqrt{3+\sqrt{5}}\right)}{\sqrt{\left(3-\sqrt{5}\right).\left(3+\sqrt{5}\right)}}\)
\(=\frac{\sqrt{5}\left(\sqrt{3+\sqrt{5}}\right)}{\sqrt{9-5}}=\frac{\sqrt{5}\left(\sqrt{3+\sqrt{5}}\right)}{\sqrt{4}}=\frac{\sqrt{5}\left(\sqrt{3+\sqrt{5}}\right)}{2}\)