DT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
W
4
AK
12 tháng 3 2018
NX : Số hạng đầu tiên có mẫu : 1 . 2
=> Số hạng thứ 100 có mẫu : 100 . ( 100 + 1 ) = 100 . 101
Ta có dãy số :
1/1 . 2 + 1/2 . 3 + 1/3 . 4 + ...+ 1/100 . 1/101
= 1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 + ...+ 1/100 - 1/101
= 1 - 1/101
= 101/101 - 1/101
= 100/101
Vậy tổng 100 số hạng đầu tiên là 100/101
12 tháng 3 2018
số hạng thứ 100 của dãy là \(\frac{1}{100\cdot101}\)
tổng của 100 số hạng đầu tiên của dãy :
\(\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+...+\frac{1}{100\cdot101}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{100}-\frac{1}{101}\)
\(=1-\frac{1}{101}\)
\(=\frac{100}{101}\)
OA
0
BM
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
13 tháng 10 2017
Gọi tổng trên là A
\(3A=1.2.3+2.3.3+3.4.3+...+n.\left(n+1\right).3\)
\(\Rightarrow3A=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+n.\left(n+1\right).\left[\left(n+2\right)-\left(n-1\right)\right]\)
\(\Rightarrow3A=1.2.3-1.2.3+2.3.4-2.3.4+3.4.5+...-\left(n-1\right).n.\left(n+1\right)+n.\left(n+1\right).\left(n+2\right)\)
\(\Rightarrow3A=n.\left(n+1\right).\left(n+2\right)\Rightarrow A=\frac{n.\left(n+1\right).\left(n+2\right)}{3}\)
NT
1
20 tháng 4 2016
C=1*2+2*3+3*4+...+98*99
C=2+6+12+...+9702
C=2+9702
C=9704
vay C=9704
D=(1*99+2*99+3*99+...+99*99)-(1*2+2*3+3*4+...+98*99)
D=(99+198+297+...+9801)-(2+6+12+...+9702)
D=(99+9801)-(2+9702)
D=9900-9704
D=196
vay D=196
ai di qua dong tinh thi nho h cho minh nhe
10 tháng 6 2016
Thừa số thứ nhất của mẫu số của phân số thứ 100 là:
\(\left(100-1\right):1+1=100\)
=> Mẫu số của phân số thứ 100 là 100.101
Tổng 100 số hạng đầu tiên:
\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{100.101}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{100}-\frac{1}{101}\)
\(=1-\frac{1}{101}=\frac{100}{101}\)
b) Ta xét mẫu số của các số hạng trong dãy :
6 = 1.6
66 = 6.11
176 = 11.16
336 = 16.21
........
Thừa số thứ nhất của mẫu của phân số thứ 100 của dãy là:
\(\left(100-1\right).5+1=496\)
=> Mẫu của phân số thứ 100 là 496.501.
Tính tổng 100 số hạng đầu:
\(\frac{1}{1.6}+\frac{1}{6.11}+\frac{1}{11.16}+\frac{1}{16.21}+...+\frac{1}{496.501}\)
\(=1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+\frac{1}{11}-\frac{1}{16}+\frac{1}{16}-\frac{1}{21}+...+\frac{1}{496}-\frac{1}{501}\)
\(=1-\frac{1}{501}=\frac{500}{501}\)
PH
3
1 tháng 2 2016
S = 1.2 + 2.3 + 3.4 + ..... + 99.100
=> 3S = 1.2.3 + 2.3(4 - 1) + 3.4(5 - 2) + ......... + 99.100(101 - 98)
=> 3S = 1.2.3 + 2.3.4 - 1.2.3 + 3.4.5 - 2.3.4 + ........ + 99.100.101 - 98.99.100
=> 3S = (1.2.3 + 2.3.4 + 3.4.5 + ..... + 98.99.100 + 99.100.101) - (1.2.3 + 2.3.4 + .......... + 98.99.100)
=> 3S = 99.100.101
=> S = \(\frac{99.100.101}{3}=333300\)
NT
1
21 tháng 9 2015
A=1.2+2.3+3.4+...+2015.2016
=> 3A=1.2.3+2.3.3+3.4.3+...+2015.2016.3
=> 3A=1.2.3+2.3.(4-1)+3.4.(5-2)+...+2015.2016.(2017-2014)
=>3A=1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+ 2015.2016.2017-2014.2015.2016
=> 3A=2015.2016.2017
=> A=\(\frac{2015.2016.2017}{3}=2731179360\)
.
.
LC
23 tháng 6 2015
nhân 3 vào mỗi hạng tử ta được:
3*(1.2+2.3+3.4+...+99.100)
= 1.2.(3-0)+ 2.3.(4-1)+ 3.4.(5-2)+... + 99.100.(101-98)
=1.2.3 + 2.3.4 -1.2.3 + 3.4.5 -2.3.4 +... + 99.100.101 - 98.99.100
= 99.100.101
Vậy tổng ban đầu 99.100.101/3= 33.100.101
Vậy tổng trên chia hết cho 2;3;4;5;10
MC
6 tháng 5 2016
A = 1.2 + 2.3 + 3.4 + ....... + 99.100
3A = 1.2.3 + 2.3.3 + 3.4.3 + ....... + 99 . 100 . 3
3A = 1.2.3 + 2.3.(4-1) + 3.4.(5-2) +.... + 99.100.(101-98)
3A = 1.2.3 + 2.3.4 - 1.2.3 + 3.4.5 - 2.3.4 + ..... + 99 . 100 . 101 - 98 . 99 . 100
3A = (1.2.3 - 1.2.3) + (2.3.4-2.3.4) + ... + (98.99.100 - 98.99.100) + 99 . 100 . 101
3A = 99 . 100 . 101 = 999900
A = 999900 : 3 = 333300
6 tháng 5 2016
A=1*2+2*3+3*4+...+99*100
A=100*101*102:3
A=343400(công thức)
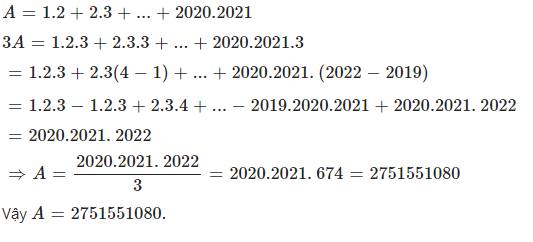
3E=1.2.3+2.3.3+3.4.3+...+2020.2021.3=
=1.2.3+2.3.(4-1)+3.4.(5-2)+...+2020.2021.(2022-2019)=
=1.2.3-1.2.3+2.3.4-2.3.4+3.4.5-...-2019.2020.2021+2020.2021.2022=
=2020.2021.2022
=> E=2020.2021.2022:3=674.2020.2021
\(E=1.2+2.3+3.4+...+2020.2021\)
\(3E=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+....+2020.2021.\left(2022-2019\right)\)
\(3E=1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+2020.2021.2022-2019.2020.2021\)
\(3E=2020.2021.2022\)
\(E=2020.2021.674\)