DQ
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
11 tháng 1 2024
Đổi 30 phút = 0,5 giờ
Quãng sông từ A đến B dài là:
\(x\) \(\times\) 0,5 + y \(\times\) 1 = 0,5\(x\) + y (km)
Kết luận Quãng đường từ A đên B dài: 0,5\(x\) + y (km)
AH
Akai Haruma
Giáo viên
31 tháng 1 2024
Lời giải:
Áp dụng tính chất tổng 3 góc trong 1 tam giác bằng $180^0$
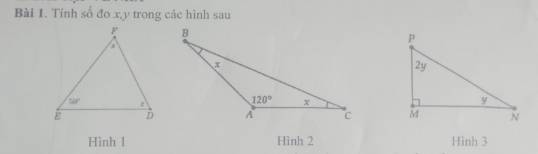
Hình 1: Hình không rõ ràng. Bạn xem lại.
Hình 2: $x+x+120^0=180^0$
$2x+120^0=180^0$
$2x=60^0$
$x=60^0:2=30^0$
Hình 3:
$2y+y+90^0=180^0$
$3y=180^0-90^0=90^0$
$y=90^0:3=30^0$
(
KV
25 tháng 1 2024
\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)
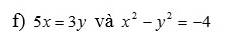
A B C D I M H N E
a/
Xét tg vuông ABD có
\(\sin\widehat{B}=\dfrac{AD}{AB}=\dfrac{12}{13}\)
\(\sin\widehat{BAD}=\sin\left(\dfrac{\Pi}{2}-\widehat{B}\right)=\cos\widehat{B}\)
Ta có
\(\sin^2\widehat{B}+\cos^2\widehat{B}=1\Rightarrow\cos^2\widehat{B}=1-\sin^2\widehat{B}=1-\left(\dfrac{12}{13}\right)^2=\dfrac{25}{169}\)
\(\Rightarrow\sin\widehat{BAD}=\cos\widehat{B}=\sqrt{\dfrac{25}{169}}\)
\(\Rightarrow\sin\widehat{BAD}=\dfrac{BD}{AB}=\dfrac{BD}{13}=\sqrt{\dfrac{25}{169}}\)
\(\Rightarrow BD=13.\sqrt{\dfrac{25}{169}}=5cm\)
Xét tg cân ABC có
\(BD=CD=\dfrac{1}{2}BC\) (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường trung tuyến)
\(\Rightarrow BC=2.BD=2.5=10cm\)
b/
Xét tg BDM có
\(BI=MI\left(gt\right);DI\perp BM\) => tg BDM cân tại D (trong tg đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)
\(\Rightarrow DM=BD=\dfrac{1}{2}BC\)
c/
Ta có
\(DM=BD\left(cmt\right);BD=CD\left(cmt\right)\Rightarrow DM=BD=CD\)
=> tg BDM và tg CDM đều là tg cân tại D
Xét tg BCM có
\(\widehat{BMC}=\left(\widehat{BMD}+\widehat{CMD}\right)=180^o-\left(\widehat{ABC}+\widehat{BCM}\right)\)
Mà \(\widehat{BMD}=\widehat{ABC};\widehat{CMD}=\widehat{BCM}\) (góc ở đáy tg cân)
\(\Rightarrow\widehat{BMC}=180^o-\left(\widehat{BMD}+\widehat{CMD}\right)=180^o-\widehat{BMC}\)
\(\Rightarrow2\widehat{BMC}=180^o\Rightarrow\widehat{BMC}=\dfrac{180^o}{2}=90^o\Rightarrow CM\perp AB\)
Mà \(AD\perp BC\)
=> H là trực tâm của tg ABC \(\Rightarrow BN\perp AC\) (trong tg 3 đường cao đồng quy)
Xét tg vuông BCM và tg vuông BCN có
BC chung
\(\widehat{ABC}=\widehat{ACB}\) (góc ở đáy tg cân)
=> tg BCM = tg BCN (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)
\(\Rightarrow BM=CN\) mà AB=AC (gt)
\(\Rightarrow\dfrac{BM}{AB}=\dfrac{CN}{AC}\) => MN//BC (Talet đảo) (1)
Xét tứ giác BDME có
BI=MI (gt); EI=DI (gt) => BDME là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> ME//BD (Trong hbh các cặp cạnh đối // với nhau từng đôi một)
=> ME//BC (2)
Từ (1) và (2) \(\Rightarrow MN\equiv ME\) (Từ 1 điểm bên ngoài 1 đường thẳng chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng cho trước)
=> E; M; N thẳng hàng
1: ΔABC cân tại A có AD là đường cao
nên D là trung điểm của BC
Xét ΔADB vuông tại D có \(sinABD=\dfrac{AD}{AB}=\dfrac{12}{13}\)
=>\(sinABC=\dfrac{12}{13}\)
=>\(cosABC=\sqrt{1-\left(\dfrac{12}{13}\right)^2}=\dfrac{5}{13}\)
Xét ΔABC có \(cosABC=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
=>\(\dfrac{13^2+BC^2-13^2}{2\cdot13\cdot BC}=\dfrac{5}{13}\)
=>\(BC^2=\dfrac{5}{13}\cdot26\cdot BC=10BC\)
=>\(BC^2-10BC=0\)
=>BC(BC-10)=0
=>BC-10=0
=>BC=10(cm)
2: Xét ΔDIB vuông tại I và ΔDIM vuông tại I có
DI chung
IB=IM
Do đó: ΔDIB=ΔDIM
=>DB=DM
mà DB=1/2BC
nên DM=1/2BC
3: Xét ΔMBC có
MD là đường trung tuyến
\(MD=\dfrac{1}{2}BC\)
Do đó: ΔMBC vuông tại M
=>CM\(\perp\)AB tại M
Xét ΔIME vuông tại I và ΔIBD vuông tại I có
IM=IB
IE=ID
Do đó: ΔIME=ΔIBD
=>\(\widehat{IME}=\widehat{IBD}\)
=>ME//BD
=>ME//BC
Xét ΔABC có
AD,CM là các đường trung tuyến
AD cắt CM tại H
Do đó: H là trực tâm của ΔABC
=>BH\(\perp\)AC tại N
Xét ΔABN vuông tại N và ΔACM vuông tại M có
AB=AC
\(\widehat{BAN}\) chung
Do đó: ΔABN=ΔACM
=>AN=AM
Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC
Ta có: MN//BC
ME//BC
MN,ME có điểm chung là M
Do đó: N,M,E thẳng hàng