Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Dấu hiệu: điểm thi học kì môn Lý của mỗi bạn học sinh lp 7 của trường THCS Chu Văn An
b, - Số các giá trị :120
- Số các giá trị khác nhau: 7
c, Bảng ''tần số''
| giá trị (x) | 3 | 5 | 6 | 7 | 8 | 9 | 10 | |
| tần số (n) | 3 | 19 | 38 | 23 | 15 | 12 | 10 | N= 120 |
d, Rút ra nhận xét:
- Có tất cả 120 giá trị nhưng chỉ có 7 giá trị khác nhau
- Điểm 3 là điểm thấp nhất (3 bạn)
- Chỉ có 10 bạn đạt được điểm tối đa (10 bạn )
- Đa số các bạn được từ 6 đến 9 điểm
c,
\(\overline{X}\)= \(\dfrac{3.3+5.19+6.38+7.23+8.15+9.12+10.10}{120}\)= \(\dfrac{821}{120}\)\(\approx\)6,8
d, \(_{M0}\)= 6

a. Dấu hiệu: Thời gian làm bài tập của 30 học sinh.
b.
| Giá trị (x) | 5 | 7 | 8 | 9 | 10 | 14 | |
| Tần số (n) | 4 | 3 | 8 | 8 | 4 | 3 | N = 30 |
Nhận xét:
- Có 4 học sinh làm bài nhanh nhất (3 phút).
- Có 3 học sinh làm bài lâu nhất (14 phút).
- Số học sinh làm bài trong 8, 9 phút chiếm đa số.
c.
x = \(\frac{5\times4+7\times3+8\times8+9\times8+10\times4+14\times3}{30}\)
\(\approx\)8,63
Mốt của dấu hiệu là: Mo = 8 và 9
a/ Dấu hiệu ở đây là thời gian giải một bài toán (tính bằng phút) của 30 học sinh
b/ Lập bảng tần số
| giá trị (x) | 5 | 7 | 8 | 9 | 10 | 14 | |
| tần số (n) | 4 | 3 | 8 | 8 | 4 | 3 | N=30 |
* nhận xét
- Thời gian làm bài ít nhất là 5 phút (có 4 học sinh)
- Thời gian làm bài nhiều nhất là 14 phút ( có 3 học sinh)
- thời gian làm bài nhiều nhất là 14 phút (có 8 học sinh)
c/ tính trung bình cộng
\(\)\(X=\frac{5.4+7.3+8.8+9.8+10.4+14.3}{30}\approx8,63\)
VẬY số trung bình cộng là 8,63
bài toán có hai mốt: M0=8 & M0=9
d/ tự vẽ
e/ Khi mỗi giá trị của dấu hiệu đều giảm 1,5 lần thì số TBC mới giảm 1,5 lần
Nếu mỗi giá trị của dấu hiệu tăng 2 đơn vị thì số TBC tăng thêm 2 đơn vị

Là bảng số liệu thống kê ban đầu bn nhé.
CHÚC BẠN HC TỐT NHA!
cong bảng như thế này là bảng j z nhok hanahmoon
| 1 | 2 | 3 | 4 |
| 5 | 5 | 2 | 3 |
bảng j z

Vì mỗi giá trị của x ta xác định được chỉ một giá trị của y tương ứng nên đại lượng y là hàm số của đại lượng x
Vì mỗi giá trị của x ta xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.

\(\overline{X}=\frac{x_1n_1+x_2n_2+....+x_kn_k}{N}\)
Ta có : \(6,8=\frac{5n+6.5+9.2+10.1}{n+5+2+1}\)
\(\Rightarrow6,8=\frac{5n+30+18+10}{n+8}\)
\(\Rightarrow6,8=\frac{5n+58}{n+8}\)
\(\Rightarrow6,8\left(n+8\right)=5n+58\)
\(\Rightarrow6,8n+54,4=5n+58\)
\(\Rightarrow6,8n-5n=58-54,4\)
\(\Rightarrow1,8n=3,6\)
\(\Rightarrow n=2\)

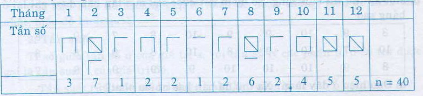
Kết quả thống kê được ngày, tháng, năm sinh của các bạn trong lớp em như sau (được làm dưới hình thức là bảng tần số):
| Tháng | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Tần số | 3 | 5 | 8 | 6 | 2 | 1 | 4 | 9 | 5 | 6 | 3 | 5 | N = 57 |

Từ hàm số đã cho, lần lượt thay các giá trị x, y đã cho trong bảng vào hàm sôs trên để tìm các giá trị còn lại. Ta được bảng sau:
|
x |
-0,5 |
-3 |
0 |
4,5 |
9 |
|
y |
−13−13 |
-2 |
0 |
3 |
6 |
 .
.
Dài quá vậy
Chia bớt đi
nó mang cả đề cương vô hay sao ý