Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\overline{X}=\frac{x_1n_1+x_2n_2+....+x_kn_k}{N}\)
Ta có : \(6,8=\frac{5n+6.5+9.2+10.1}{n+5+2+1}\)
\(\Rightarrow6,8=\frac{5n+30+18+10}{n+8}\)
\(\Rightarrow6,8=\frac{5n+58}{n+8}\)
\(\Rightarrow6,8\left(n+8\right)=5n+58\)
\(\Rightarrow6,8n+54,4=5n+58\)
\(\Rightarrow6,8n-5n=58-54,4\)
\(\Rightarrow1,8n=3,6\)
\(\Rightarrow n=2\)
Từ cột thứ 6 ta tính được hệ số a từ công thức y =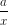 
;
a = 4.1,5 = 6.Từ đó tính được các số còn lại. Ta được bảng sau:
a) Đặt P(x) = 0. Ta có:
\(2x+\dfrac{1}{2}=0\)
\(\Rightarrow2x=-\dfrac{1}{2}\)
\(\Rightarrow x=-\dfrac{1}{4}\)
Vậy nghiệm của P(x) là \(x=-\dfrac{1}{4}\)
b) Q(x) = x2 - 2x - 3 = x(x - 2) - 3
Đặt Q(x) = 0. Ta có:
x(x - 2) - 3 = 0
=> x(x - 2) = 3
=> Ta có các trường hợp:
+/ x = 1; x - 2 = 3 => x = 5
Mà \(1\ne5\) nên không tồn tại trường hợp x = 1; x - 2 = 3
+/ x = -1; x - 2 = -3 => x = -1 (chọn)
+/ x = 3; x - 2 = 1 => x = 3 (chọn)
+/ x = -3; x - 2 = -1 => x = 1
Mà \(-3\ne1\) nên không tồn tại trường hợp x = -3; x - 2 = -1
Vậy nghiệm của Q(x) là x = -1 hoặc x = 3
Vậy có thể tìm nghiệm của đa thức bằng cách đặt đa thức bằng 0
a/ Dấu hiệu mà bạn An quan tâm là: thời gian cần thiết để đi từ nhà đến trường
b/ Giá trị khác nhau: 5
c/ Các giá trị khác nhau: 17;18;19;20;21
| Giá trị (x) | Tần số (N) |
| 17 | 1 |
| 18 | 3 |
| 19 | 3 |
| 20 | 2 |
| 21 | 1 |
| N = 10 |
) và nêu nhận xét
Thanks nhìu
Là bảng số liệu thống kê ban đầu bn nhé.
CHÚC BẠN HC TỐT NHA!
cong bảng như thế này là bảng j z nhok hanahmoon
bảng j z