Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

| 110 | 110 | 110 | 110 | 115 | 115 |
| 115 | 115 | 115 | 115 | 115 | 120 |
| 120 | 120 | 120 | 120 | 120 | 120 |
| 120 | 120 | 125 | 125 | 125 | 125 |
| 125 | 125 | 125 | 125 | 130 | 130 |

a) xy = 2.36 = 3.24 = 6. 12 = 8.9 = 9.8 = 72
Vậy hai đại lượng x,y trong bảng a là hai đại lượng tỉ lệ nghịch.
b) x.y = 1. 60 = 2. 30 = 3.20 = 4. 15 ≠ 5. 14
Vậy hai đại lượng x, y trong bảng b là hai đại lượng không phải là tỉ lệ nghịch.

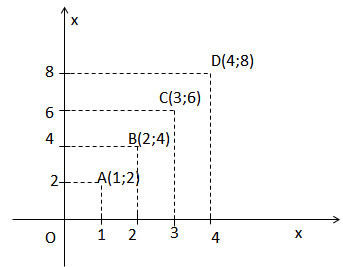
a) Tất cả các cặp giá trị tương ứng (x;y) là: (0;0), (1;2); (2; 4); (3; 6); (4; 8).
b) Trên hình vẽ 0, A, B, C, D là vị trí của các điểm biểu diễn các cặp giá trị tương ứng của x và y trong câu a.
a) Tất cả các cặp giá trị tương ứng (x;y) là: (0;0), (1;2); (2; 4); (3; 6); (4; 8).
b) Trên hình vẽ 0, A, B, C, D là vị trí của các điểm biểu diễn các cặp giá trị tương ứng của x và y trong câu a.


a) Vì với mọi giá trị của x ta xác định được chỉ một giá trị tương ứng của y , nên đại lượng y là hàm số của đại lượng x. b) Đại lượng y là hàm số của đại lượng x

a) Vì với mọi giá trị của x ta xác định được chỉ một giá trị tương ứng của y, nên đại lượng y là hàm số của đại lượng x.
b) Đại lượng y là hàm số của đại lượng x.
a) Vì mọi giá trị của x ta xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.
b) Đại lượng y là hàm số của đại lượng x.

Từ cột thứ 6 ta tính được hệ số a từ công thức y = 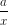 ;
;
a = 4.1,5 = 6.Từ đó tính được các số còn lại. Ta được bảng sau:
![]()

| x | -5 | -3 | -1 | 1 | 3 | 5 | 15 |
| y=f(x) | -3 | -5 | -15 | 15 | 5 | 3 | 1 |
f (-3)=-5 f(6)=\(\dfrac{5}{2}\)
a)
| x | -5 | -3 | -1 | 1 | 3 | 5 | 15 |
|
y=f(x) |
-3 | -5 | -15 | 15 | 5 | 3 | 1 |
b) f(-3)=-5
f(6)=\(\dfrac{5}{2}\)
Từ hàm số đã cho, lần lượt thay các giá trị x, y đã cho trong bảng vào hàm sôs trên để tìm các giá trị còn lại. Ta được bảng sau:
x
-0,5
-3
0
4,5
9
y
−13−13
-2
0
3
6