Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
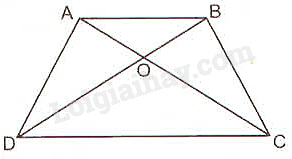
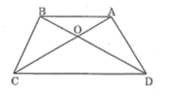
Xét tam giác \(OCD\) có \(AB//CD\) (giả thiết) và \(AB\) cắt \(OC;OD\) lần lượt tại \(A;B\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{AB}}{{CD}} \Rightarrow \frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} \Rightarrow OA.OD = OB.OC\) (điều phải chứng minh).
Xét tam giác \(OCD\) có \(AB//CD\) (giả thiết) và \(AB\) cắt \(OC;OD\) lần lượt tại \(A;B\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{AB}}{{CD}} \Rightarrow \frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} \Rightarrow OA.OD = OB.OC\) (điều phải chứng minh).
a) Trong tam giác ADC, ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ABC
⇒ EI // CD (tính chất đường trung bình của tam giác)
Trong tam giác ABC ta có:
I là trung điểm của AC
F là trung điểm của BC
Nên IF là đường trung bình của ∆ ABC
⇒ IF // AB (tính chất đường trung bình của tam giác)
b) Câu b đou
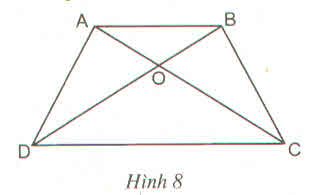
a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:
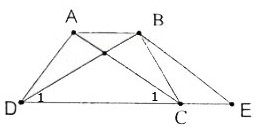
AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra 
= 
(3)
∆BDE cân tại B (câu a) nên 
= (4)
Từ (3) và (4) suy ra =
Xét ∆ACD và ∆BCD có AC = BD (gt)
= (cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra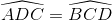 
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Bài giải:
a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:
AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra = (3)
∆BDE cân tại B (câu a) nên = (4)
Từ (3) và (4) suy ra =
Xét ∆ACD và ∆BCD có AC = BD (gt)
= (cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra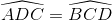
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
A B C D O
Ta có: \(AB//CD\left(Gt\right)\)
Áp dụng định lí ta - let trong hình thang \(ABCD\)ta có:
\(\Rightarrow\frac{OA}{OC}=\frac{OB}{OD}\Rightarrow OA.OD=OB.OC\left(đpcm\right)\)
Ta có: AB // CD (gt), áp dụng hệ quả của định lý Ta – lét ta có:
Suy ra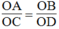
(hệ quả định lí ta-lét)
Vậy OA.OD = OB.OC