Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có, theo quy tắc ba điểm của phép trừ:
=
–
(1)
Mặt khác, =
(2)
Từ (1) và (2) suy ra:
=
–
.
b) Ta có : =
–
(1)
=
(2)
Từ (1) và (2) cho ta:
=
–
.
c) Ta có :
–
=
(1)
–
=
(2)
=
(3)
Từ (1), (2), (3) suy ra đpcm.
d) –
+
= (
–
) +
=
+
=
+
( vì
=
) =

Ta có: BC2 = AC2 + AB2 – 2AB.AC. cos1200
=> BC2 = m2 + n2 – 2m.n ()
=> BC2 = m2 + n2 + m.n
=> BC =
Ta có
a2 = 82 + 52 – 2.8.5 cos 1200 = 64 + 25 + 40 = 129
=> a = √129 ≈ 11, 36cm
Ta có thể tính góc B theo định lí cosin
cosB = =
≈ 0,7936 =>
= 37048’
Ta cũng có thể tính góc B theo định lí sin :
cosB = =
=> sinB ≈ 0,6085 =>
= 37048’
Tính C từ = 1800– (
+
) =>
≈ 22012’

Từ định lí cosin a2 = b2 + c2 – 2bc. cosA
ta suy ra cos A = =
=> cosA ≈ 0,8089 => = 360
Tương tự, ta tính được ≈ 1060 28’ ;
≈ 370 32’.

a) Gọi theo thứ tự ∆1, ∆2, ∆3 là giá của các vectơ ,
,
cùng phương với
=> ∆1 //∆3 ( hoặc ∆1 = ∆3 ) (1)
cùng phương với
=> ∆2 // ∆3 ( hoặc ∆2 = ∆3 ) (2)
Từ (1), (2) suy ra ∆1 // ∆2 ( hoặc ∆1 = ∆2 ), theo định nghĩa hai vectơ ,
cùng phương.
Vậy
a) đúng.
b) Đúng.

a) Nối BM
Ta có AM= AB.cosMAB
=> || = |
|.cos(
,
)
Ta có: .
= |
|.|
| ( vì hai vectơ
,
cùng phương)
=> .
= |
|.|
|.cosAMB.
nhưng ||.|
|.cos(
,
) =
.
Vậy .
=
.
Với .
=
.
lý luận tương tự.

b) .
=
.
.
=
.
=> .
+
.
=
(
+
)
=> .
+
.
=
= 4R2

Trước hết ta có
= 3
=>
= 3 (
+
)
=> = 3
+ 3
=> – = 3
=> =
mà =
–
nên
=
(
–
)
Theo quy tắc 3 điểm, ta có
=
+
=>
=
+
–
=> = –
+
hay
= –
+

Gọi G là giao điểm của AK, BM thì G là trọng tâm của tam giác.
Ta có =
=>
=
= –
= –
= –
Theo quy tắc 3 điểm đối với tổng vec tơ:
=
+
=>
=
–
=
(
–
).
AK là trung tuyến thuộc cạnh BC nên
+
= 2
=>
–
+
= 2
Từ đây ta có =
+
=>
= –
–
.
BM là trung tuyến thuộc đỉnh B nên
+
= 2
=> –
+
= 2
=> =
+
.

Ta có cos(,
) = cos1350 =
sin(,
) = sin900 = 1
cos(,
) = cos00 = 1

Ta có: = 1800 – (
+
) = 400
Áp dụng định lí sin :
=
=
, ta có:
b = ≈ 212,32cm
c = ≈ 179,40cm
Ta có: AQ = ABcot480
AP = ABcot350
QP = AB(cot350 – cot480)
=> AB =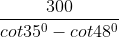 ≈
≈ 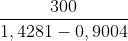
Tính được AB ≈ 568,50m