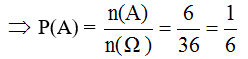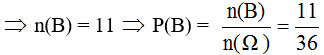Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tập hợp A gồm các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc.
A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}
a) Trong các số 1, 2, 3, 4, 5, 6, có hai số là hợp số là: 4, 6.
Vậy có hai kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là hợp số” là: mặt 4 chấm, mặt 6 chấm (lấy ra từ tập hợp A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}).
b) Trong các số 1, 2, 3, 4, 5, 6, có hai số chia 3 dư 1 là: 1, 4.
Vậy có hai kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chia 3 dư 1” là: mặt 1 chấm, mặt 4 chấm (lấy ra từ tập hợp A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}).
c) Trong các số 1, 2, 3, 4, 5, 6, có ba số là ước của 4 là: 1, 2, 4.
Vậy có ba kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là ước của 4” là: mặt 1 chấm, mặt 2 chấm, mặt 4 chấm (lấy ra từ tập hợp A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}).

a: n(omega)=6
n(A)=1
=>P(A)=1/6
b: B={2;4;6}
=>n(B)=3
=>P(B)=3/6=1/2

- Biến cố A là biến cố ngẫu nhiên vì nếu ta gieo được 2 lần cùng ra 1 thì tích của chúng sẽ không lớn hơn 1.
- Biến cố B là biến cố chắc chắn vì mặt có số chấm ít nhất là 1 nếu ta gieo 2 lần thì ít nhất chúng ta có kết quả là 2 nên tổng sẽ lớn hơn 1.
- Biến cố C là biến cố không thể do các mặt của xúc xắc là 1,2,3,4,5,6 mà trong các số này không có tích 2 số nào là 7.
- Biến cố D là biến cố ngẫu nhiên vì các mặt của xúc xắc là 1,2,3,4,5,6 mà trong các số này có rất nhiều số có tổng là 7 ví dụ như 1 và 6, 2 và 5 nhưng cũng có nhiều cặp số không có tổng là 7 như 3 và 1, 1 và 2.

Trong các số 1, 2, 3, 4, 5, 6, có ba số nguyên tố là 2, 3, 5.
Vậy có ba kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số nguyên tố” là: mặt 2 chấm, mặt 3 chấm, mặt 5 chấm. (Lấy ra từ tập hợp A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}).

Gọi X là tập hợp các kết quả có thể xảy ra.
Ta có \(X=\left\{\left(1;1\right);\left(1;2\right);\left(1;3\right);...;\left(6;6\right)\right\}\). Ta thấy tập hợp trên có 36 phần tử, hoặc 36 kết quả có thể xảy ra.
a) Biến cố trên có thể xảy ra nếu xảy ra 1 trong các kết quả sau:
(4;6); (5;5); (6;4). Có 3 kết quả để biến cố trên xảy ra.
Vậy xác suất của biến cố trên là \(\dfrac{3}{36}=\dfrac{1}{12}\).
b) Biến cố trên có thể xảy ra nếu xảy ra 1 trong các kết quả sau:
(1;2); (2;1); (1;4); (2;3); (3;2); (4;1); (1;6); (2;5); (3;4); (4;3); (5;2); (6;1); (3;6); (4;5); (5;4); (6;3); (5;6); (6;5). Có 18 kết quả để biến cố trên xảy ra.
Vậy xác suất để biến cố trên xảy ra là \(\dfrac{18}{36}=\dfrac{1}{2}\).

a: \(\Omega=\left\{1;2;3;4;5;6\right\}\)
=>n(omega)=6
A={1;4}
=>n(A)=2
=>P(A)=2/6=1/3
b: B={3;4;5;6}
=>n(B)=4
=>P(B)=4/6=2/3

a. Không gian mẫu gồm 36 kết quả đồng khả năng xuất hiện, được mô tả như sau:
Ta có: Ω = {(i, j) | 1 ≤ i , j ≤ 6}, trong đó i, j lần lượt là số chấm xuất hiện trong lần gieo thứ nhất và thứ hai, n(Ω) = 36.
b. A = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)} => n(A) = 6
B = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 5)}