
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


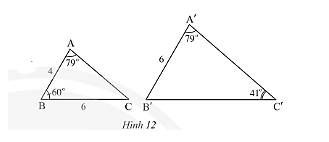
a) Xét tam giác \(A'B'C'\) ta có:
\(\widehat {A'} + \widehat {B'} + \widehat {C'} = 180^\circ \)
Thay số: \(79^\circ + \widehat {B'} + 41^\circ = 180^\circ \)
\( \Rightarrow \widehat {B'} = 180^\circ - 79^\circ - 41^\circ = 60^\circ \)
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) ta có:
\(\widehat A = \widehat {A'} = 79^\circ \) (giả thuyết)
\(\widehat B = \widehat {B'} = 60^\circ \) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta A'B'C'\) (g.g)
b) Vì \(\Delta ABC\backsim\Delta A'B'C'\) nên \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) (các cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{4}{6} = \frac{6}{{B'C'}} \Rightarrow B'C' = \frac{{6.6}}{4} = 9\)
Vậy \(B'C' = 9\).

Câu hỏi của pham trung thanh - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo lời giải tại link trên nhé.

Cho tam giác ABC vuông tại A có đường cao AH
a) chứng minh tam giác AHB đồng dạng với tam giác ABC
b) Cho BC = 10cm AB = 6cm Tính AC, HB
c) Phân giác của góc ABC cắt AH tại F và cắt cạnh AC tại E. Chứng minh
FA/FH =EC/EA
d) Đường thẳng qua C song song vs BE cắt AH tại K. CHứng minh: AF2 = FH x FK
chịu
botay.com.vn

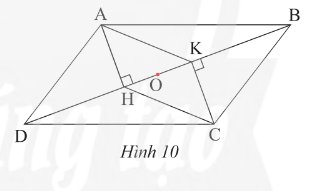
a/ Xét tg vuông AHD và tg vuông AKB có
\(\widehat{BAK}+\widehat{ABC}=90^o\)
\(\widehat{DAH}+\widehat{ADC}=90^o\)
Mà \(\widehat{ABC}=\widehat{ADC}\) (Hai góc đối của hbh)
\(\Rightarrow\widehat{DAH}=\widehat{BAK}\)
=> tg AHD đồng dạng với tg AKB \(\Rightarrow\frac{AH}{AK}=\frac{DA}{AB}\) mà AB = DC (hai cạnh đối của hbh) \(\Rightarrow\frac{AH}{AK}=\frac{DA}{DC}\left(dpcm\right)\)
b/ Ta có K và H đều nhìn AC dưới 1 góc 90 độ
=> Tứ giác AKCH là tứ giác nội tiếp đường tròn đường kính AC
=> sđ \(\widehat{AKH}\) = sđ \(\widehat{ACH}\) = 1/2 sđ cung AH (Góc nội tiếp đường tròn) \(\Rightarrow\widehat{AKH}=\widehat{ACH}\left(dpcm\right)\)

a,xét ΔABC và ΔAHC, có:
góc BAC=góc AHC(=90 độ)
góc C chung
=>ΔABC đồng dạng ΔAHC(g-g)

Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\) (1)
Vì \(AKCH\) là hình bình hành (gt)
Mà \(O\) là trung điểm của \(AC\)
Suy ra \(O\) là trung điểm của \(HK\)
Vì \(\left\{ \begin{array}{l}BC \bot AB'\\B'C' \bot AB'\end{array} \right. \Rightarrow BC//B'C'\)(quan hệ từ vuông góc đến song song).
- Xét tam giác \(AB'C'\) có \(BC//B'C'\) và \(BC\) cắt \(AB';AC'\) lần lượt tại \(B;C\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AB'}} = \frac{{BC}}{{B'C'}} \Rightarrow \frac{x}{{x + h}} = \frac{a}{{a'}} \Rightarrow xa' = a\left( {x + h} \right) \Leftrightarrow xa' = ax + ah\)
\( \Leftrightarrow xa' - ax = ah \Leftrightarrow x\left( {a' - a} \right) = ah \Leftrightarrow x = \frac{{ah}}{{a' - a}}\) (điều phải chứng minh).