Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(x^2\ge0\forall x\in R\Rightarrow\)
\(y=-x^2\le0\forall x\in R\)
Vậy \(Maxy=0\Leftrightarrow x=0\)
Dễ thấy Với \(x^2\) càng lớn thì $y$ càng bé nên y bé nhất trong đoạn từ -3 đến 2 là $x=-3$ $ \Leftrightarrow Min=-(-3)^2=-9$
KL:................

a) Vì đồ thị hàm số đi qua A(1;-1) nên ta có :
x= 1 ; y=-1 và thay vào hàm số ta có
y= (2a+3) <=> -1 = (2a + 3)*1 <=> 2a + 3 = -1 <=> 2a = - 3 - 1 <=> 2a = -4 <=> a = -2
Vậy đồ thị hàm số có dạng y = ( -4 +3)x = -1x
- Ta có phương trình hoành độ giao điểm :
-1x = 4x - 5
<=> -1x - 4x = -5
<=>-5x = -5 <=> x = 1 => y = -1x = -1 * 1 = -1
Vậy 2 đồ thị hàm số giao nhau tại B ( 1; -1)
b) Vì hoành độ bằng 1 bằng 1 nên x = 1
Ta có phương trình hoành độ giao điểm :
(2a + 3 )x = -2x +2
thay x = 1 vào phương trình ta có :
( 2a + 3)*1 = -2*1 + 2
<=> 2a + 3 = -2+ 2
<=> 2a = -2 +2 -3 <=> a = \(-\frac{3}{2}\)

a/ Hàm số đi qua A(2,7)
\(\Rightarrow7=-2a+5\)
\(\Leftrightarrow a=-1\)
b/ Thay \(x=1+\sqrt{3}\), \(y=4-\sqrt{3}\)ta được
\(4-\sqrt{3}=-\left(1+\sqrt{3}\right)a+5\)
\(\Leftrightarrow a=1\)

Giả sử đồ thị hàm số đã cho luôn đi qua điểm cố định \(\left(x_0,y_0\right)\)với mọi \(m\).
\(y_0=\left(3m^2+1\right)x_0+m^2-4,\forall m\)
\(\Leftrightarrow m^2\left(3x_0+1\right)+x_0-y_0-4=0,\forall m\)
\(\Leftrightarrow\hept{\begin{cases}3x_0+1=0\\x_0-y_0-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x_0=-\frac{1}{3}\\y_0=-\frac{13}{3}\end{cases}}\)
Vậy điểm cố định mà đồ thị hàm số đã cho luôn đi qua có tọa độ là \(\left(-\frac{1}{3},-\frac{13}{3}\right)\).

- Lập bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = -0,75x2 | -12 | -3 | 0 | -3 | -12 |
- Vẽ đồ thị:
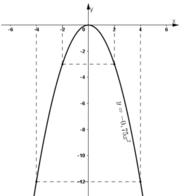
- Quan sát đồ thị hàm số y = -0,75x2:
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.

Ta có đồ thị hàm số $y=x^2$
Suy ra Giá trị lớn nhất trong đoạn từ $-3$ đến $2$ là $9$ khi $x=-3$
Giá trị nhỏ nhất trong đoạn từ $-3$ đến $2$ là $0$ khi \(x=0\)