Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vẽ đồ thị: y = -0,75x2
| x | -4 | -2 | -1 | 0 | 1 | 2 | 4 |
| y=-0,75x2 | -12 | -3 | -0,75 | 0 | -0,75 | -3 | -12 |
Vì -2 < 0 < 4 và khi x = 0 thì y = 0 là giá trị lớn nhất của hàm số. Hơn nữa khi x = -2 thì y = -0,75 . (-2)2 = -3, khi x = 4 thì y = -0,75 . (4)2 = -12 < -3
Do đó khi -2 ≤ x ≤ 4 thì giá trị nhỏ nhất của hàm số là -12 còn giá trị lớn nhất là 0.

- Lập bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = - 0 , 75 x 2 | -12 | -3 | 0 | -3 | -12 |
- Vẽ đồ thị:
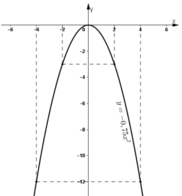
- Quan sát đồ thị hàm số y = - 0 , 75 x 2 :
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.

Ta có \(x^2\ge0\forall x\in R\Rightarrow\)
\(y=-x^2\le0\forall x\in R\)
Vậy \(Maxy=0\Leftrightarrow x=0\)
Dễ thấy Với \(x^2\) càng lớn thì $y$ càng bé nên y bé nhất trong đoạn từ -3 đến 2 là $x=-3$ $ \Leftrightarrow Min=-(-3)^2=-9$
KL:................

Bài giải:
a) Thế x = 4 và y = 11 vào y = 3x +b ta có: 11 = 3.4 + b ⇔ b = -1. Khi đó hàm số đã cho trở thành: y = 3x – 1. Đây là đường thẳng đi qua 2 điểm A(0;-1) và B(1/3; 0)
b) Đồ thị hàm số y = ax + 5 đi qua điểm A(-1; 3) nên: 3 = a(-1) + 5
<=> a = 2
Khi đó hàm số đã cho trở thành : y = 2x + 5. Đây là đường thẳng đi qua hai điểm A(0; 5) và B (−52;0)(−52;0)
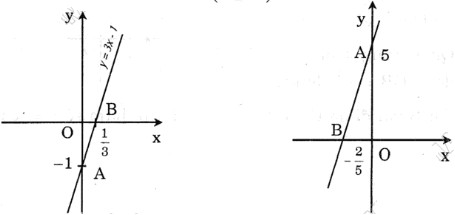

Lời giải
a) Hàm số bậc nhất đồng biến khi (a>0) => m-3 >0 => m>3
b) A(1;2) => y(1) =2 => (m-3).1=2 => m=5
c) B(1;-2) => y(1) =-2=> (m-3).1=-2 => m=1
d) 
a) Hàm số \(y=\left(m-3\right)x\) đồng biến khi \(m-3>0\Leftrightarrow m>3\)
Hàm số \(y=\left(m-3\right)x\) nghịch biến khi \(m-3< 0\Leftrightarrow m< 3\)


- Lập bảng giá trị:
- Vẽ đồ thị:
- Quan sát đồ thị hàm số y = -0,75x2:
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.