TF
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2023
10.
\(H\left(x\right)=-5x^4+10x^3-15x+1\)
\(=-5x\left(x^3-2x^2+3\right)+1\)
\(=-5x.0+1\)
\(=1\)
9.
\(P\left(x\right)-Q\left(x\right)=\left(1-a\right)x^3+x^2+x-6\)
\(P\left(x\right)-Q\left(x\right)\) là đa thức bậc 3 khi và chỉ khi \(1-a\ne0\)
\(\Rightarrow a\ne1\)
DT
3
17 tháng 8 2019
Ta có: \(14x=21y=16z\)=> \(\frac{x}{\frac{1}{14}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}\) => \(\frac{2x}{\frac{1}{7}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{2x}{\frac{1}{7}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}=\frac{2x+y-z}{\frac{1}{7}+\frac{1}{21}-\frac{1}{16}}=\frac{2}{\frac{43}{336}}=\frac{672}{43}\)
=> \(\hept{\begin{cases}\frac{x}{\frac{1}{14}}=\frac{672}{43}\\\frac{y}{\frac{1}{21}}=\frac{672}{43}\\\frac{z}{\frac{1}{16}}=\frac{672}{43}\end{cases}}\) => \(\hept{\begin{cases}x=\frac{672}{43}.\frac{1}{14}=\frac{48}{43}\\y=\frac{672}{43}.\frac{1}{21}=\frac{32}{43}\\z=\frac{672}{43}.\frac{1}{16}=\frac{42}{43}\end{cases}}\)
Vậy ...
17 tháng 8 2019
\(\Rightarrow\frac{x}{\frac{1}{14}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}\)
\(\Rightarrow\frac{2x}{\frac{1}{7}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}\)
+ Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{2x}{\frac{1}{7}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}=\frac{2x+y-z}{\frac{1}{7}+\frac{1}{21}-\frac{1}{16}}=\frac{2}{\frac{43}{336}}=\frac{672}{43}\)
Suy ra \(\frac{2x}{\frac{1}{7}}=\frac{672}{43}\Rightarrow x=\frac{48}{43}\)
\(\frac{y}{\frac{1}{21}}=\frac{672}{43}\Rightarrow y=\frac{32}{43}\)
\(\frac{z}{\frac{1}{16}}=\frac{672}{43}\Rightarrow z=\frac{42}{43}\)
Vậy \(x=\frac{48}{43};y=\frac{32}{43};z=\frac{42}{43}\)
Chúc bạn học tốt !!!
BV
3
13 tháng 4 2023
`7,`
`a, B+A=4x-2x^2+3`
`-> B=(4x-2x^2+3)-A`
`-> B=(4x-2x^2+3)-(x^2-2x+1)`
`B=4x-2x^2+3-x^2+2x-1`
`B=(-2x^2-x^2)+(4x+2x)+(3-1)`
`B=-3x^2+6x+2`
`b, C-A=-x+7`
`-> C=(-x+7)+A`
`-> C=(-x+7)+(x^2-2x+1)`
`-> C=-x+7+x^2-2x+1`
`C=x^2+(-x-2x)+(7+1)`
`C=x^2-3x+8`
`c,`
`A-D=x^2-2`
`-> D= A- (x^2-2)`
`-> D=(x^2-2x+1)-(x^2-2)`
`D=x^2-2x+1-x^2+2`
`D=(x^2-x^2)-2x+(1+2)`
`D=-2x+3`
13 tháng 4 2023
`6,`
`a,`
`P+Q=4x-2x^2+3`
`-> Q=(4x-2x^2+3)-P`
`-> Q=(4x-2x^2+3)-(3x^2+x-1)`
`Q=4x-2x^2+3-3x^2-x+1`
`Q=(-2x^2-3x^2)+(4x-x)+(3+1)`
`Q=x^2+3x+4`
`b,`
`x^2-5x+2-P=H`
`-> H= (x^2-5x+2)-(3x^2+x-1)`
`H=x^2-5x+2-3x^2-x+1`
`H=(x^2-3x^2)+(-5x-x)+(2+1)`
`H=-4x^2-6x+3`
`c,`
`P-R=5x^2-3x-4`
`-> R= P- (5x^2-3x-4)`
`-> R=(3x^2+x-1)-(5x^2-3x-4)`
`R=3x^2+x-1-5x^2+3x+4`
`R=(3x^2-5x^2)+(x+3x)+(-1+4)`
`R=-2x^2+4x+3`
TN
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
30 tháng 9 2024
Các em đăng câu hỏi lên diễn đàn thì cần đăng đầy đủ nội dung câu hỏi lên trên này. Có như vậy mọi người mới biết yêu cầu của đề bài và trợ giúp các em tốt nhất. Cảm ơn các em đã đồng hành cùng Olm.
BN
1
13 tháng 10 2021
a) \(\Rightarrow\left(x-3\right)\left(x+4\right)=5.12\)
\(\Rightarrow x^2+x-72=0\)
\(\Rightarrow\left(x-8\right)\left(x+9\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-9\end{matrix}\right.\)
b) \(\Rightarrow\left(x+3\right)^2=36\)
\(\Rightarrow\left[{}\begin{matrix}x+3=6\\x+3=-6\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-9\end{matrix}\right.\)
c) \(\Rightarrow2x^2=8\Rightarrow x^2=4\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
MH
22 tháng 10 2021
\(\dfrac{x}{y}=\dfrac{5}{2}\) ⇒\(\dfrac{x}{5}=\dfrac{y}{2}\)
\(\dfrac{y}{z}=\dfrac{1}{3}\) ⇒\(\dfrac{y}{1}=\dfrac{z}{3}\) ⇒\(\dfrac{y}{2}=\dfrac{z}{6}\)
⇒\(\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{z}{6}\) ⇒\(\dfrac{x^2}{25}=\dfrac{y^2}{4}=\dfrac{2z^2}{72}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x^2}{25}=\dfrac{y^2}{4}=\dfrac{2z^2}{72}=\dfrac{x^2-y^2+2z^2}{25-4+72}=\dfrac{372}{93}=4\)
⇒\(\left\{{}\begin{matrix}x=4.5=20\\y=4.2=8\\z=4.6=24\end{matrix}\right.\)
NK
1
23 tháng 9 2023
Bạn cần bài nào ạ? Nếu bạn cần giúp tất cả thì bạn tách ra từng CH khác nhau nhé!
NT
4
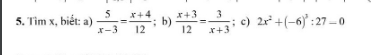
Lời giải:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x+2020|+|x+2021|=|x+2020|+|-(x+2021)|$
$\geq |x+2020-(x+2021)|=1$
Vậy GTNN của biểu thức là $1$. Giá trị này đạt tại $(x+2020).-(x+2021)\geq 0$
$(x+2020)(x+2021)\leq 0$
$-2021\leq x\leq -2020$