Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{2x+1}{4}\)-\(\frac{y-2}{3}\)=\(\frac{1}{12}\)
=\(\frac{3.\left[2x+1\right]}{12}\)-\(\frac{4.\left[y-2\right]}{12}\)=\(\frac{1}{12}\)
=6x+3-4y-6=1
=6x-3-4y=1
=6x-4y=4
=2[3x-2y]=4
MK MỚI HỌC LỚP 8 ,CHÚA SẼ CHUYỂN HỆ PHƯƠNG TRÌNH CUỐI CÙNG ,BẠN GIẢI NỐT NHA

Bạn chỉ cần vào cái ô đầu tiên trên thanh công cụ trên trang này là ghi được dấu căn rồi

\(A=\left(\dfrac{\sqrt{x}-2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right):\dfrac{2\sqrt{x}}{x-1}\)
\(=\left(\dfrac{\sqrt{x}-2}{\sqrt{x}^2+2\sqrt{x}+1^2}-\dfrac{\sqrt{x}+2}{\sqrt{x}^2-1^2}\right).\dfrac{x-1}{2\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right).\dfrac{x-1}{2\sqrt{x}}\)
Tới đây là có được mẫu chung ở dấu = thứ 2 rồi.
\(A=\left(\dfrac{\sqrt{x}-2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right):\dfrac{2\sqrt{x}}{x-1}\) ( với x>0;\(x\ne1\) )
\(=\left[\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right].\dfrac{x-1}{2\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(x-1\right)}.\dfrac{x-1}{2\sqrt{x}}\)
\(=.....\) ( theo như trên )

Ta có: \(\left\{{}\begin{matrix}5\left(x+2y\right)=3x-8\\2x+4=3x-15y-12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x+10y-3x=-8\\2x-3x+15y=-12-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+10y=-8\\-x+15y=-16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+5y=-4\\-x+15y=-16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}20y=-20\\x+5y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=-4-5y=-4-5\cdot\left(-1\right)=-4+5=1\end{matrix}\right.\)
Vậy: (x,y)=(1;-1)
$\begin{cases}5(x+2y)=3x-8\\2x+4=3x-15y-12\end{cases}$
`<=>` $\begin{cases}5x+10y=3x-8\\x-15y=16\end{cases}$
`<=>` $\begin{cases}2x+10y=-8\\x-15y=16\end{cases}$
`<=>` $\begin{cases}x+4y=-4\\x-15y=16\end{cases}$
`<=>` $\begin{cases}19y=-20\\x=15y+16\end{cases}$
`<=>` $\begin{cases}y=-\dfrac{20}{19}\\x=\dfrac{4}{19}\end{cases}$

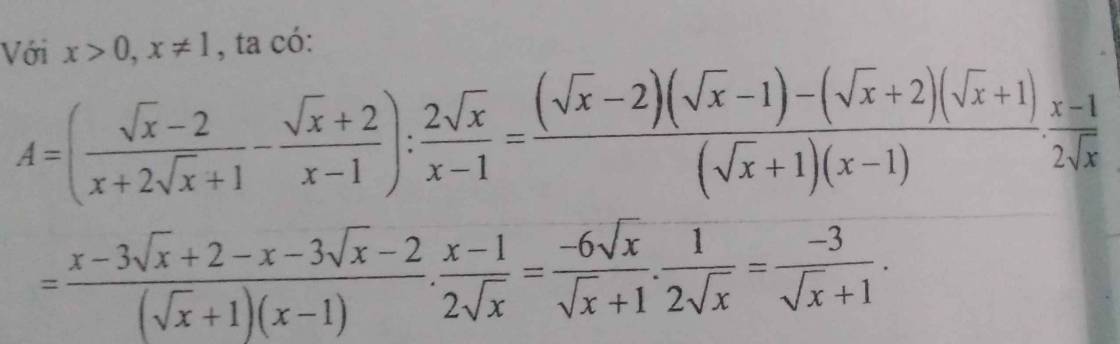
{ : ngoặc kép
<=> : tương đương
\(\hept{ }\): dấu ngoặc kép
<=> : Tương đương
\({}\)