NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H9
HT.Phong (9A5)
CTVHS
10 tháng 1 2024
Bài 2:
\(\dfrac{12}{-24}=\dfrac{12:12}{-24:12}=\dfrac{1}{-2}\)
\(\dfrac{-39}{75}=\dfrac{-39:3}{75:3}=\dfrac{-13}{25}\)
\(\dfrac{132}{-264}=\dfrac{132:132}{-264:132}=\dfrac{1}{-2}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
10 tháng 1 2024
Bài 3:
\(\dfrac{1}{-2}=\dfrac{-1}{2};\dfrac{-3}{-5}=\dfrac{3}{5};\dfrac{2}{-7}=\dfrac{-2}{7}\)
Bài 4:
\(15p=\dfrac{1}{4}h;20p=\dfrac{1}{3}h;45p=\dfrac{3}{4}h;50p=\dfrac{5}{6}h\)
H9
HT.Phong (9A5)
CTVHS
12 tháng 1 2024
2. Các cặp số đối với nhau là:
\(\dfrac{-5}{6}\) và \(\dfrac{5}{6}\)
\(\dfrac{-40}{-10}\) và \(\dfrac{40}{-10}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 1 2024
Bài 4:
a; \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) = \(\dfrac{5}{20}\) - \(\dfrac{4}{20}\) = \(\dfrac{1}{20}\)
b; \(\dfrac{3}{5}\) - \(\dfrac{-1}{2}\) = \(\dfrac{6}{10}\) + \(\dfrac{5}{10}\) = \(\dfrac{11}{10}\)
c; \(\dfrac{3}{5}\) - \(\dfrac{-1}{3}\) = \(\dfrac{9}{15}\) + \(\dfrac{5}{15}\) = \(\dfrac{14}{15}\)
d; \(\dfrac{-5}{7}\) - \(\dfrac{1}{3}\)= \(\dfrac{-15}{21}\) - \(\dfrac{7}{21}\)= \(\dfrac{-22}{21}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 1 2024
Bài 5
a; 1 + \(\dfrac{3}{4}\) = \(\dfrac{4}{4}\) + \(\dfrac{3}{4}\) = \(\dfrac{7}{4}\) b; 1 - \(\dfrac{1}{2}\) = \(\dfrac{2}{2}\) - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\)
c; \(\dfrac{1}{5}\) - 2 = \(\dfrac{1}{5}\) - \(\dfrac{10}{5}\) = \(\dfrac{-9}{5}\) d; -5 - \(\dfrac{1}{6}\) = \(\dfrac{-30}{6}\) - \(\dfrac{1}{6}\) = \(\dfrac{-31}{6}\)
e; - 3 - \(\dfrac{2}{7}\)= \(\dfrac{-21}{7}\) - \(\dfrac{2}{7}\)= \(\dfrac{-23}{7}\) f; - 3 + \(\dfrac{2}{5}\) = \(\dfrac{-15}{5}\) + \(\dfrac{2}{5}\)= - \(\dfrac{13}{5}\)
g; - 3 - \(\dfrac{2}{3}\) = \(\dfrac{-9}{3}\) - \(\dfrac{2}{3}\) = \(\dfrac{-11}{3}\) h; - 4 - \(\dfrac{-5}{7}\) = \(\dfrac{-28}{7}\)+ \(\dfrac{5}{7}\) = - \(\dfrac{23}{7}\)
AH
Akai Haruma
Giáo viên
4 tháng 2 2024
Bài 5:
a. Gọi $d=ƯCLN(n-2, n+1)$
$\Rightarrow n-2\vdots d; n+1\vdots d$
$\Rightarrow (n+1)-(n-2)\vdots d$
$\Rightarrow 3\vdots d\Rightarrow d\in \left\{1; 3\right\}$
Để ps tối giản thì $n-2\not\vdots 3$
$\Leftrightarrow n\neq 3k+2$ với $k$ là số tự nhiên bất kỳ.
b.
Gọi $d=ƯCLN(n+5, n-2)$
$\Rightarrow n+5\vdots d; n-2\vdots d$
$\Rightarrow (n+5)-(n-2)\vdots d$
$\Rightarrow 7\vdots d$
$\Rightarrow d\in \left\{1; 7\right\}$
Để ps tối giản thì $n-2\not\vdots 7$
$\Rightarrow n\neq 7k+2$ với $k$ là số tự nhiên bất kỳ.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 1 2024
Bài 1:
a; 24 ⋮ \(x\); 30 ⋮ \(x\); 48 \(⋮\) \(x\) và \(x\) lớn nhất.
vì 24 \(⋮\) \(x\); 30 ⋮ \(x\); 48 ⋮ \(x\) ⇒ \(x\) \(\in\) ƯC(24; 30; 48)
Vì \(x\) là lớn nhât nên \(x\) \(\in\) ƯCLN(24; 30; 48)
24 = 22.33; 30 = 2.3.5; 48 = 24.3
ƯCLN(24; 30; 48) = 2.3 = 6
⇒ \(x\) = 6
Vậy \(x\) = 6
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 1 2024
b; 120 ⋮ \(x\); 180 ⋮ \(x\); 30 ⋮ \(x\)
⇒ \(x\) \(\in\) ƯC(120; 180; 390)
120 = 23.3.5; 180 = 22.32.5; 390 = 2.3.5.13
ƯC(120; 180; 390) = 2.3.5 = 30
⇒ \(x\in\) Ư(30) = {1; 2; 3; 5; 6; 10;15; 30}
Vì 5 ≤ \(x\) ≤ 15 nên \(x\) \(\in\) {5; 6; 10; 15}
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
11 tháng 1 2024
Bài 2:
Chiều cao trung bình của 8 bạn trong tổ 1 là:
115 : 8 = \(\dfrac{115}{8}\) (dm)
Chiều cao trung bình của 10 bạn trong tổ 2 là:
138 : 10 = \(\dfrac{69}{5}\) (dm)
\(\dfrac{115}{8}\) = \(\dfrac{115\times5}{8\times5}\) = \(\dfrac{575}{40}\)
\(\dfrac{69}{5}\) = \(\dfrac{69\times8}{5\times8}\) = \(\dfrac{552}{40}\)
Vì \(\dfrac{575}{40}\) > \(\dfrac{552}{40}\)
Vậy chiều cao trung bình của các bạn tổ 1 lớn hơn chiều cao trung bình của các bạn tổ 2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
11 tháng 1 2024
Bài 3:
a; \(\dfrac{-11}{5}\) < \(\dfrac{-10}{5}\) = -2
\(\dfrac{-7}{4}\) > \(\dfrac{-8}{4}\) = - 2
\(\Rightarrow\) \(\dfrac{-11}{5}\) < \(\dfrac{-7}{4}\)
b; \(\dfrac{2020}{-2021}\) > - 1
\(\dfrac{-2022}{2021}\) < -1
Vậy \(\dfrac{2020}{-2021}\) > \(\dfrac{-2022}{2021}\)
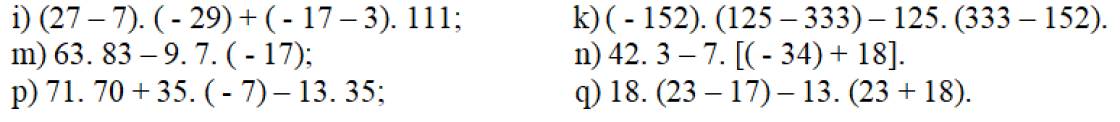
i: =20*(-29)+(-20)*111
=20(-29-111)
=-20*140=-2800
k: \(=-152\cdot125+152\cdot333-125\cdot333+125\cdot152\)
=27*333
=8991
m: \(=63\left(83+17\right)=6300\)
n: \(=126-7\cdot\left(-16\right)=126+112=238\)
p: \(=35\left(71\cdot2-7-13\right)=35\cdot122=4270\)
q: \(=18\cdot23-18\cdot17-13\cdot23-13\cdot18=5\cdot23-18\cdot30=115-540=-425\)