Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt 
, tìm điều kiện của t.
Đưa về bất phương trình dạng 
Cách giải :
Ta có 
Đặt 
, khi đó phương trình trở thành
Ta có: 
Vậy 
a) 2 (x + 5) - x2 - 5x = 0
=> 2 (x + 5) - (x2 + 5x) = 0
=> 2 (x + 5) - x (x + 5) = 0
=> (2 - x) (x + 5) = 0
Có 2 TH xảy ra :
TH1 : 2 - x = 0 => x = 2
TH2 : x + 5 = 0 => x = -5
a, 2\((\)x +5\()\) - x2 - 5x =0
\(\Leftrightarrow\) 2x2 +10-x2 - 5x=0
\(\Leftrightarrow\)x2 - 5x +10=0
\(\Delta'\) = \((\) -5\()\)2 - 1. 10=15 \(\Rightarrow\) \(\sqrt{\Delta'}\) = \(\sqrt{15}\)
\(\Rightarrow\) x1 = 5 + \(\sqrt{15}\) ; x2 = 5- \(\sqrt{15}\)
pt có 2 nghiệm ........
b, 2x2 + 3x -5 =0
có a+b+c= 2+3+ \((\) -5\()\) =0
\(\Rightarrow\) x1=1 , x2 =\(\dfrac{-5}{2}\)
c, \((\) x-1\()\)2 + 4.\((x+2)\) - \((x^2-3)\)=0
\(\Rightarrow x^2-2x+1+4x+8-x^{2^{ }}+3=0\)
\(\Leftrightarrow\) -2x +12 =0
\(\Leftrightarrow\)-2x=-12\(\Leftrightarrow\) x= 6
bạn ơi, xem lại đề ra 1 chút, hình như có câu sai đề thì phải
a) \(4x-7>0\Leftrightarrow4x>7\)\(\Leftrightarrow x>\frac{7}{4}\)
b) \(-5x+8>0\Leftrightarrow5x<8\Leftrightarrow x<\frac{8}{5}\)
c)\(9x-10\le0\Leftrightarrow9x\le10\)\(\Leftrightarrow x\le\frac{10}{9}\)
d) \(\left(x+1\right)^2+4\le x^2+3x+10\)\(\Leftrightarrow x^2-2x+1+4\le x^2+3x+10\)
\(\Leftrightarrow5x\ge-5\Leftrightarrow x\ge-1\)
a,
4x - 7 > 0
↔ 4x > 7
↔ x > \(\dfrac{7}{4}\)
Vậy tập nghiệm của bất phương trình là S = { x / x>\(\dfrac{7}{4}\) }
b,
-5x + 8 > 0
↔ 8 > 5x
↔ \(\dfrac{8}{5}\) > x
Vậy tập nghiệm của bất phương trình là S = { x / \(\dfrac{8}{5}\) > x }
c,
9x - 10 ≤ 0
↔ 9x ≤ 10
↔ x ≤ \(\dfrac{10}{9}\)
Vậy tập nghiệm của bất phương trình là S = { x / x ≤ \(\dfrac{10}{9}\) }
d,
( x - 1 )\(^2\) + 4 ≤ x\(^2\) + 3x + 10
↔ x\(^2\) - 2x +1 +4 ≤ x\(^2\) + 3x + 10
↔ 1 + 4 - 10 ≤ x \(^2\) - x\(^2\) + 3x + 2x
↔ -5 ≤ 5x
↔ -1 ≤ x
Vậy tập nghiệm của bất phương trình là S = { x / -1 ≤ x}
Chọn A.
ĐK: x > 2
Pt ⇔ log3(x – 2)2(x – 4)2 = 0
⇔ (x – 2)2(x – 4)2 = 1
Với 2 < x< 4 suy ra (x - 2)(4 - x) = 1 ⇔ x = 3 (tm)
Với x ≥ 4 suy ra (x - 2)(x - 4) = 1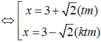 
Suy ra (x1 – x2)2 = (3 – 3 – √2)2 = 2
Chọn B.
Phương pháp:
Đưa phương trình về dạng tích, giải phương trình tìm nghiệm và tìm điều kiện để bài toán thỏa.
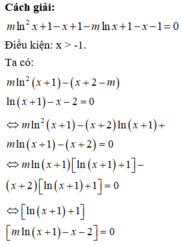
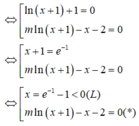
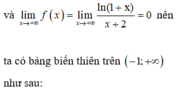
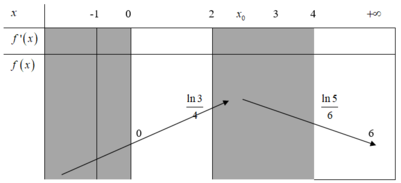
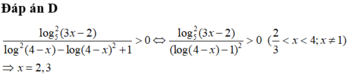
Đáp án D
Hai phương trình tương đương là hai phương trình có cùng tập nghiệm.