Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:

Thời gian xem ti vi trung bình trong tuần trước của các bạn học sinh này là:\({\rm{\;}}\bar x = \frac{{8 \times 2.5 + 16 \times 7.5 + 4 \times 12.5 + 2 \times 17.5 + 2 \times 22.5}}{{8 + 16 + 4 + 2 + 2}} = 8.4375\) (giờ).

Tham khảo:
a)

b) Không thể tính chính xác, chúng ta chỉ có thể tinh số gần đúng thời gian tự học trung bình của các học sinh trong lớp
c) Giá trị đại diện của nhóm bằng trung bình giá trị đầu mút phải và trái của nhóm đó
Nhóm \( \ge 4.5\) là nhóm mở nên ta dựa theo nhóm gần đó nhất là nhóm [3;4.5) để lấy giá trị đại diện

Số trung binh của mẫu số liệu: : \(\bar x = \frac{{0.75 \times 8 + 2.25 \times 23 + 2.75 \times 6 + 5.25 \times 3}}{{40}} = 2.25\).

Cỡ mẫu n = 42.
Trung vị \({M_e}\) là \(\frac{{{x_{21}} + {x_{22}}}}{2}\). Do \({x_{21}},\;{x_{22}}\) đều thuộc nhóm \(\left[ {40;60} \right)\) nên nhóm này chứa trung vị.
Đáp án: C.

Cỡ mẫu n = 42.
Tứ phân vị thứ nhất \({Q_1}\) là \(\frac{{{x_{10}} + {x_{11}}}}{2}\). Do \({x_{10}},\;{x_{11}}\) đều thuộc nhóm \(\left[ {20;40} \right)\) nên nhóm náy chứa \({Q_1}\).
Đáp án: B.

Tần số của nhóm \(\left[ {40;60} \right)\) lớn nhất (=12) nên mốt thuộc nhóm \(\left[ {40;60} \right)\).
Đáp án: B.

Vì đây là mẫu số liệu ghép nhóm và tần số các nhóm khác nhau nên có 1 mốt
Đáp án: B.

Không gian mẫu là số cách chọn ngẫu nhiên 3 học sinh từ 13 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 3 học sinh được chọn có cả nam và nữ đồng thời có cả khối 11 và khối 12
Ta có các trường hợp thuận lợi cho biến cố A là:
● Trường hợp 1. Chọn 1 học sinh khối 11; 1 học sinh nam khối 12 và 1 học sinh nữ khối 12 nên có ![]() cách.
cách.
● Trường hợp 2. Chọn 1 học sinh khối 11; 2 học sinh nữ khối 12 có ![]() cách.
cách.
● Trường hợp 3. Chọn 2 học sinh khối 11; 1 học sinh nữ khối 12 có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là ![]()
Vậy xác suất cần tính 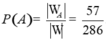
Chọn D.

Số cách chọn 8 học sinh gồm hai khối là phần bù của cách chọn 8 học sinh đi dự đại hội sao cho mỗi khối có ít nhất 1 học sinh được chọn.( chú ý mỗi khối đều có ít hơn 8 học sinh).
Số cách chọn 8 học sinh từ hai khối là: ![]() .
.
Số cách chọn 8 học sinh bất kì là: ![]()
Số cách chọn thỏa yêu cầu bài toán: ![]()
Chọn D.
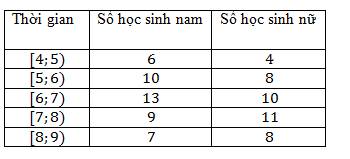


Tham khảo:
a)
Thời gian ngủ trung bình của các bạn nam
\({\bar x_{nam}} = \frac{{4.5 \times 6 + 5.5 \times 10 + 6.5 \times 13 + 7.5 \times 9 + 8.5 \times 7}}{{6 + 10 + 13 + 9 + 7}} = 6.52\).
Thời gian ngủ trung bình của các bạn nữ:
\({\bar x_{nữ}} = \frac{{4.5 \times 4 + 5.5 \times 8 + 6.5 \times 10 + \times 7.5 \times 11 + 8.5 \times 8}}{{4 + 8 + 10 + 11 + 8}} = 6.77\).
6.77 > 6.52. Như vậy thời gian ngủ trung bình của các bạn nữ nhiều hơn các bạn nam.
b) Cỡ mẫu n = 86
Tứ phân vị thứ nhất \({Q_1}\) là \(\frac{{{x_{21}} + {x_{22}}}}{2}\). Do \({x_{21}},\;{x_{22}}\) đều thuộc nhóm \(\left[ {5;6} \right)\) nên nhóm này chứa \({Q_1}\). Do đó, \(p = 2;\;\;{a_2} = 5;\;\;{m_2} = 18;\;\;{m_1} = 10;\;{a_3} - {a_2} = 1\)
Ta có: \({Q_1} = 5 + \frac{{\frac{{86}}{4} - 10}}{{18}} \times 1 = 5.64\)
Ý nghĩa: Có 75% học sinh khối 1 ngủt nhất 5.64 giờ.