Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

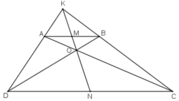
Gọi KO cắt AB, CD lần lượt tại M, N.
ΔKDN có AM // DN (A ∈ KD, M ∈ KN) ⇒ 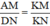 (Hệ quả định lý Ta-let)
(Hệ quả định lý Ta-let)
ΔKCN có BM // CN (M ∈ KN, B ∈ KC) ⇒ 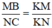 (Hệ quả định lý Ta-let)
(Hệ quả định lý Ta-let)
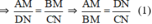
ΔOCN có AM // NC (A ∈ OC, M ∈ ON) ⇒ 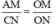 (Hệ quả định lý Ta-let)
(Hệ quả định lý Ta-let)
ΔODN có MB // ND (M ∈ ON, B ∈ OD) ⇒ 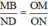 (Hệ quả định lý Ta-let)
(Hệ quả định lý Ta-let)
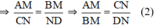
Từ (1) và (2) suy ra 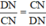 ⇒ CN = DN ⇒ AM = MB
⇒ CN = DN ⇒ AM = MB
Vậy M, N là trung điểm AB, CD.

A B C D N K M O
Gọi KO cắt AB, CD lần lượt tại M, N.
ΔKDN có AM // DN (A ∈ KD, M ∈ KN) ⇒ \(\frac{AM}{DN}=\frac{KM}{KN}\)( hệ quả của định lí Talet )
ΔKCN có BM // CN (M ∈ KN, B ∈ KC) ⇒ \(\frac{MB}{NC}=\frac{KM}{KN}\)( hệ quả của định lí Talet )
\(\Rightarrow\frac{AM}{DN}=\frac{BM}{CN}\Rightarrow\frac{AM}{BM}=\frac{DN}{CN}\left(1\right)\)
.ΔOCN có AM // NC (A ∈ OC, M ∈ ON) ⇒ \(\frac{AM}{CN}=\frac{ON}{CN}\)( hệ quả của định lí Talet )
ΔODN có MB // ND (M ∈ ON, B ∈ OD) ⇒ \(\frac{MB}{ND}=\frac{OM}{ON}\)( hệ quả của định lí Talet )
\(\Rightarrow\frac{AM}{CN}=\frac{BM}{ND}\Rightarrow\frac{AM}{BM}=\frac{CN}{DN}\left(2\right)\)
Từ (1)(2) , suy ra :
\(\frac{DN}{CN}=\frac{CN}{DN}\Rightarrow CN=DN\Rightarrow AM=MB\)
Vậy M, N là trung điểm AB, CD.

Vì OE // DC ==> OA/AC = OE/DC (định lý Ta-let) (1)
Vì OF // DC ==> OB/BD = OF/DC (định lý Ta-let) (2)
Vì AB // CD ==> OA/OC = OB/OD (định lý ta-let)
Theo tính chất dãy tỉ số bằng nhau ta có:
OA/OC = OB/OD <=> OA / (OA + OC) = OB / (OB + OD)
<=> OA / AC = OB / BD (3)
Từ (1), (2) và (3) suy ra ta có:
OE / DC = OF / DC <=> OE = OF (đpcm)

Gọi H là trung điểm DC.
Chứng minh HE// IF( vì cùng //BC)
=> HE vuông FK ( vì FK vuông IF)
Tương tự HF// EI( vì cùng //AD)
=> HF vuông EK( vì EK vuông IE)
Xét tam giác EFH có EK và FK là 2 đường cao nên K là trực tâm. Suy ra HK vuông FE mà FE //DC nên HK vuông DC tại H suy ra tam giác KDC cân tại K. Nên KD=KC

Bạn tự vẽ hình nhé
Xét \(\Delta ACD\) có OE // CD(gt)
=> \(\dfrac{OE}{DC}=\dfrac{AO}{AC}\left(1\right)\)
Xét \(\Delta BCD\) có OF // CD (gt)
=> \(\dfrac{OF}{DC}=\dfrac{BF}{FC}\left(2\right)\)
Mặt khác AB // CD nên \(\dfrac{AO}{AC}=\dfrac{BF}{FC}\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
=> \(\dfrac{OE}{DC}=\dfrac{OF}{DC}\) => OE = OF

Trong ΔDAB, ta có: OM // AB (gt)
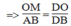 (Hệ quả định lí Ta-lét) (1)
(Hệ quả định lí Ta-lét) (1)
Trong ΔCAB, ta có: ON // AB (gt)
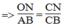 (Hệ quả định lí Ta-lét) (2)
(Hệ quả định lí Ta-lét) (2)
Trong ΔBCD, ta có: ON // CD (gt)
Suy ra: ![]() (định lí Ta-lét) (3)
(định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra: 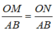
Vậy: OM = ON
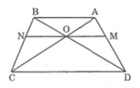
Ta có EO//DC ⇒ OE/DC = AO/AC (1)
OF//DC ⇒ OF/DC = BO/BD (2)
Ta có: AB//DC ⇒ OA/OC = OB/OD
⇒ OA/ (OC + OA) = OB/(OD+ OB) ⇒ OA/AC = OB/BD (3)
Từ (1),(2),(3) ta có OE/DC = OF/DC ⇒ OE = OF
Ta có AB//EF
⇒ AN/EO = KN/KO và BN/FO = KM/KO
⇒ AN/EO = BN/FO ⇒ AN = BN
Tương tự: FE//DC ⇒ EO/DM = KO/KM
và FO/CM = KO/KM ⇒EO/DM=FO/CM ⇒ DM=CM